题目内容
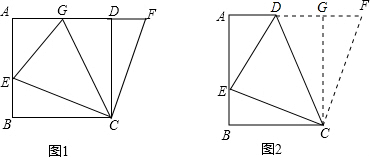
如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
（1）求证：CE=CF；
（2）图1中，若G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=6，E是AB上一点，且∠DCE=45°，BE=2，求DE的长．
（1）求证：CE=CF；
（2）图1中，若G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=6，E是AB上一点，且∠DCE=45°，BE=2，求DE的长．
（1）证明：∵四边形ABCD是正方形，
∴CB=CD，∠B=∠CDA，
∵DF=BE，
∴△CEB≌△CFD，
∴CE=CF，
（2）成立．理由如下：
过C作CG⊥DF，
证得∠ECF=90°，
∴∠FCG=45°，
证得△CEG≌△CFG（SAS），
∴GE=GF=DF+GD=BE+GD，
（3）延长AD到F，使得DF=DE，过C作CG⊥DF，
同理得：DE=DF=DG+BE=DG+2=AB-AD+2=6-AD+2=8-AD，
又∵DE=
=
，
∴
=8-AD，
∴AD=3，
∴DE=5．
∴CB=CD，∠B=∠CDA，
∵DF=BE，
∴△CEB≌△CFD，
∴CE=CF，
（2）成立．理由如下：
过C作CG⊥DF，
证得∠ECF=90°，
∴∠FCG=45°，
证得△CEG≌△CFG（SAS），
∴GE=GF=DF+GD=BE+GD，
（3）延长AD到F，使得DF=DE，过C作CG⊥DF，
同理得：DE=DF=DG+BE=DG+2=AB-AD+2=6-AD+2=8-AD，
又∵DE=
| AE2+AD2 |
| 42+AD2 |
∴
| 42+AD2 |
∴AD=3，
∴DE=5．
练习册系列答案
相关题目
