题目内容
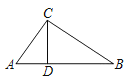
【题目】如图,在△ABC中,点D是AB边上一点(不与A,B两点重合),下列条件:①∠ACD=∠B; ②∠ADC=∠ACB;③AC2=ADAB;④![]() ,能使△ABC∽△ACD的条件的个数为( )
,能使△ABC∽△ACD的条件的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
由∠A是公共角,根据有两组角对应相等的两个三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似,判定△ABC与△ACD相似,即可得出结果.
∵∠A是公共角,
∴当∠ACD=∠B时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当∠ADC=∠ACB时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当AC2=ADAB时,即![]() ,△ADC∽△ACB(两组对应边的比相等且夹角对应相等的两个三角形相似).
,△ADC∽△ACB(两组对应边的比相等且夹角对应相等的两个三角形相似).
当![]() 时,∠A不是夹角,则不能判定△ADC与△ACB相似;
时,∠A不是夹角,则不能判定△ADC与△ACB相似;
∴能够判定△ABC与△ACD相似的条件是:①②③.
故选:C.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目