题目内容
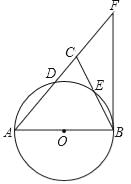
【题目】 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P为边BC上一个动点(可以包括点C但不包括点B),以P为圆心PB为半径作⊙P交AB于点D过点D作⊙P的切线交边AC于点E,
(1)求证:AE=DE;
(2)若PB=2,求AE的长;
(3)在P点的运动过程中,请直接写出线段AE长度的取值范围.
【答案】(1)详见解析;(2)AE=![]() ;(3)
;(3)![]() ≤AE<
≤AE<![]() .
.
【解析】
(1)首先得出∠ADE+∠PDB=90°,进而得出∠B+∠A=90°,利用PD=PB得∠EDA=∠A进而得出答案;
(2)利用勾股定理得出ED2+PD2=EC2+CP2=PE2,求出AE即可;
(3)分别根据当D(P)点在B点时以及当P与C重合时,求出AE的长,进而得出AE的取值范围.
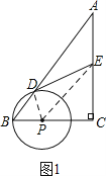
(1)证明:如图1,连接PD.
∵DE切⊙O于D.
∴PD⊥DE.
∴∠ADE+∠PDB=90°.
∵∠C=90°.
∴∠B+∠A=90°.
∵PD=PB.
∴∠PDB=∠B.
∴∠A=∠ADE.
∴AE=DE;
(2)解:如图1,连接PE,设DE=AE=x,则EC=8-x,
∵PB=PD=2,BC=6.
∴PC=4.
∵∠PDE=∠C=90°,
∴ED2+PD2=EC2+CP2=PE2.
∴x2+22=(8-x)2+42.
解得x=![]() .
.
∴AE=![]() ;
;
(3)解:如图2,当P点在B点时,此时点D也在B点,

∵AE=ED,设AE=ED=x,则EC=8-x,
∴EC2+BC2=BE2,
∴(8-x)2+62=x2,
解得:x=![]() ,
,
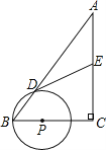
如图3,当P与C重合时,

∵AE=ED,设AE=ED=x,则EC=8-x,
∴EC2=DC2+DE2,
∴(8-x)2=62+x2,
解得:x=![]() ,
,
∵P为边BC上一个动点(可以包括点C但不包括点B),
∴线段AE长度的取值范围为:![]() ≤AE<
≤AE<![]() .
.

练习册系列答案
相关题目