ћвƒњƒЏ»Ё
°Њћвƒњ°њ‘Џ°чABC÷–£ђAC£љBC£ђ°ѕACB£љ90°г£ђDќ™AB±яµƒ÷–µг£ђ“‘Dќ™÷±љ«ґ•µгµƒRt°чDEFµƒЅнЅљЄцґ•µгE£ђFЈ÷±р¬д‘Џ±яAC£ђCB£®їтЋь√«µƒ—”≥§ѕя£©…ѕ£Ѓ
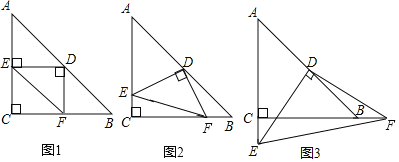
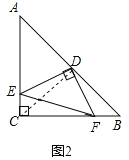
£®1£©»зЌЉ1£ђ»фRt°чDEFµƒЅљћх÷±љ«±яDE£ђDF”л°чABCµƒЅљћх÷±љ«±яAC£ђBCї•ѕаіє÷±£ђ‘тS°чDEF+S°чCEF£љ![]() S°чABC£ђ«уµ±S°чDEF£љS°чCEF£љ2 ±£ђAC±яµƒ≥§£ї
S°чABC£ђ«уµ±S°чDEF£љS°чCEF£љ2 ±£ђAC±яµƒ≥§£ї
£®2£©»зЌЉ2£ђ»фRt°чDEFµƒЅљћх÷±љ«±яDE£ђDF”л°чABCµƒЅљћх÷±љ«±яAC£ђBC≤їіє÷±£ђS°чDEF+S°чCEF£љ![]() S°чABC£ђ «Јс≥…ЅҐ£њ»ф≥…ЅҐ£ђ«лЄш”и÷§√ч£ї»ф≤ї≥…ЅҐ£ђ«л÷±љ”–і≥цS°чDEF£ђS°чCEF£ђS°чABC÷ЃЉдµƒ эЅњєЎѕµ£ї
S°чABC£ђ «Јс≥…ЅҐ£њ»ф≥…ЅҐ£ђ«лЄш”и÷§√ч£ї»ф≤ї≥…ЅҐ£ђ«л÷±љ”–і≥цS°чDEF£ђS°чCEF£ђS°чABC÷ЃЉдµƒ эЅњєЎѕµ£ї
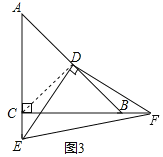
£®3£©»зЌЉ3£ђ»фRt°чDEFµƒЅљћх÷±љ«±яDE£ђDF”л°чABCµƒЅљћх÷±љ«±яAC£ђBC≤їіє÷±£ђ«“µгE‘ЏACµƒ—”≥§ѕя…ѕ£ђµгF‘ЏCBµƒ—”≥§ѕя…ѕ£ђS°чDEF+S°чCEF£љ![]() S°чABC «Јс≥…ЅҐ£њ»ф≥…ЅҐ£ђ«лЄш”и÷§√ч£ї»ф≤ї≥…ЅҐ£ђ«л÷±љ”–і≥цS°чDEF£ђS°чCEF£ђS°чABC÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
S°чABC «Јс≥…ЅҐ£њ»ф≥…ЅҐ£ђ«лЄш”и÷§√ч£ї»ф≤ї≥…ЅҐ£ђ«л÷±љ”–і≥цS°чDEF£ђS°чCEF£ђS°чABC÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
°Њір∞Є°њ£®1£©4£ї£®2£©≥…ЅҐ£ђјн”…ѕкЉыљвќц£ї£®3£©≤ї≥…ЅҐ£ђS°чDEF©БS°чCEF£љ![]() S°чABC£Ѓ
S°чABC£Ѓ
°Њљвќц°њ
£®1£©÷§√чDE «°чABCµƒ÷–ќїѕя£ђµ√≥цDE![]() BC£ђAC£љ2CE£ђЌђјнDF£љ
BC£ђAC£љ2CE£ђЌђјнDF£љ![]() AC£ђ÷§≥цЋƒ±я–ќDECF «’эЈљ–ќ£ђµ√≥цCE£љDF£љCF£љDE£ђµ√≥цS°чDEF£љS°чCEF£љ2£љ
AC£ђ÷§≥цЋƒ±я–ќDECF «’эЈљ–ќ£ђµ√≥цCE£љDF£љCF£љDE£ђµ√≥цS°чDEF£љS°чCEF£љ2£љ![]() DEDF£љ
DEDF£љ![]() DF2£ђ«у≥цDF£љ2£ђЉіњ…µ√≥цAC£љ2CE£љ4£ї
DF2£ђ«у≥цDF£љ2£ђЉіњ…µ√≥цAC£љ2CE£љ4£ї
£®2£©Ѕђљ”CD£ђ÷§√ч°чCDE°’°чBDF£ђµ√≥цS°чCDE£љS°чBDF£ђЉіњ…µ√≥цљб¬џ£ї
£®3£©≤ї≥…ЅҐ£їЅђљ”CD£ђЌђ£®2£©µ√≥ц°чDEC°’°чDBF£ђµ√≥цS°чDEF£љSќе±я–ќDBFEC£љS°чCFE+S°чDBC£љS°чCFE+![]() S°чABC£Ѓ
S°чABC£Ѓ
љв£Ї£®1£©°я°ѕACB£љ90°г£ђDE°ЌAC£ђDF°ЌBC£ђ
°аЋƒ±я–ќDECF «ЊЎ–ќ£ђ
°я°ѕACB£љ90°г£ђ
°аBC°ЌAC£ђ
°яDE°ЌAC£ђ
°аDE°ќBC£ђ
°яDќ™AB±яµƒ÷–µг£ђ
°аDE «°чABCµƒ÷–ќїѕя£ђ
°аDE£љ![]() BC£ђAC£љ2CE£ђ
BC£ђAC£љ2CE£ђ
Ќђјн£ЇDF£љ![]() AC£ђ
AC£ђ
°яAC£љBC£ђ
°аDE£љDF£ђ
°аЋƒ±я–ќDECF «’эЈљ–ќ£ђ
°аCE£љDF£љCF£љDE£ђ
°яS°чDEF£љS°чCEF£љ2£љ![]() DEDF£љ
DEDF£љ![]() DF2£ђ
DF2£ђ
°аDF£љ2£ђ
°аCE£љ2£ђ
°аAC£љ2CE£љ4£ї
£®2£©S°чDEF+S°чCEF£љ![]() S°чABC≥…ЅҐ£ђјн”…»зѕ¬£Ї
S°чABC≥…ЅҐ£ђјн”…»зѕ¬£Ї
Ѕђљ”CD£ї»зЌЉ2Ћщ Њ£Ї
°яAC£љBC£ђ°ѕACB£љ90°г£ђDќ™AB÷–µг£ђ
°а°ѕB£љ45°г£ђ°ѕDCE£љ![]() °ѕACB£љ45°г£ђCD°ЌAB£ђCD£љ
°ѕACB£љ45°г£ђCD°ЌAB£ђCD£љ![]() AB£љBD£ђ
AB£љBD£ђ
°а°ѕDCE£љ°ѕB£ђ°ѕCDB£љ90°г£ђS°чABC£љ2S°чBCD£ђ
°я°ѕEDF£љ90°г£ђ
°а°ѕCDE£љ°ѕBDF£ђ
‘Џ°чCDEЇЌ°чBDF÷–£ђ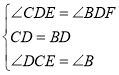 £ђ
£ђ
°а°чCDE°’°чBDF£®ASA£©£ђ
°аDE£љDF£ЃS°чCDE£љS°чBDF£Ѓ
°аS°чDEF+S°чCEF£љS°чCDE+S°чCDF£љS°чBCD£љ![]() S°чABC£ї
S°чABC£ї
£®3£©≤ї≥…ЅҐ£їS°чDEF©БS°чCEF£љ![]() S°чABC£їјн”…»зѕ¬£Ї
S°чABC£їјн”…»зѕ¬£Ї
Ѕђљ”CD£ђ»зЌЉ3Ћщ Њ£Ї
Ќђ£®1£©µ√£Ї°чDEC°’°чDBF£ђ°ѕDCE£љ°ѕDBF£љ135°г£ђ
°аS°чDEF£љSќе±я–ќDBFEC£ђ
£љS°чCFE+S°чDBC£ђ
£љS°чCFE+![]() S°чABC£ђ
S°чABC£ђ
°аS°чDEF©БS°чCFE£љ![]() S°чABC£Ѓ
S°чABC£Ѓ
°аS°чDEF°ҐS°чCEF°ҐS°чABCµƒєЎѕµ «£ЇS°чDEF©БS°чCEF£љ![]() S°чABC£Ѓ
S°чABC£Ѓ

 њмј÷–°≤© њєЃєћ”лћбЄяѕµЅ–ір∞Є
њмј÷–°≤© њєЃєћ”лћбЄяѕµЅ–ір∞Є