题目内容
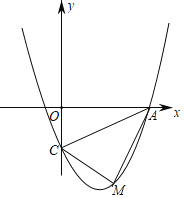
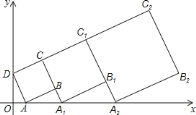
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .延长
.延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
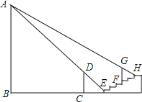
,作正方形![]() ,按这样的规律进行下去,第
,按这样的规律进行下去,第![]() 个正方形(正方形
个正方形(正方形![]() 看作第
看作第![]() 个)的面积为( )
个)的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先求出第一个正方形的边长和面积,再求出第二个正方形的边长和面积,根据第一个正方形和第二个正方形的面积得出规律,根据规律即可得出结论.
∵点A的坐标为(1,0),点D的坐标为(0,2).∠AOD=90°,
∴AD=![]() =
=![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠DAB=∠ABC=90°,AB=AD=BC=![]() ,
,
∴正方形ABCD的面积为:![]() ×
×![]() =5,∠ABB1=90°,∠OAD+∠BAA1=90°,
=5,∠ABB1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ODA∽△BAA1,
∴![]() =
=![]() =
=![]() ,
,
∴BA1=![]() ,
,
∴CA1=BC+BA1=![]() ,
,
∴第二个正方形的面积为:![]() ×
×![]() =5×
=5×![]() ,…,
,…,
得出规律,第2011个正方形的面积为:5(![]() )2010;
)2010;
故答案选:B.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
【题目】某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示:
批发价(元个) | 零售价(元/个) | |
甲型号垃圾桶 | 12 | 16 |
乙型号垃圾桶 | 30 | 36 |
若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,
(1)求y关于x的函数表达式.
(2)若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).