题目内容
【题目】在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人距B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：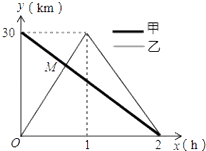 
（1）写出A、B两地之间的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义；
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．
【答案】
（1）解：x=0时，甲距离B地30千米，
所以，A、B两地的距离为30千米
（2）解：由图可知，甲的速度：30÷2=15千米/时，
乙的速度：30÷1=30千米/时，
30÷（15+30）= 
， ×30=20千米，
所以，点M的坐标为（ ，20），表示甲、乙两人出发 小时后相遇，此时距离B地20千米；
（3）解：设x小时甲、乙两人相距3km，
①若是相遇前，则15x+30x=30﹣3，解得x= 
，
②若是相遇后，则15x+30x=30+3，解得x= 
，
③若是甲到达B地前，而乙到达A地后按原路返回时，
则15x﹣30（x﹣1）=3，
解得x= 
，
所以，当 ≤x≤ 
或 ≤x≤2时，甲、乙两人能够用无线对讲机保持联系
【解析】（1）根据x=0时，甲距离B地30千米，由此即可解决问题．（2）根据相遇时间= 
即可解决．（3）分三个时间段求出时间即可，①是相遇前，则15x+30x=30﹣3，②是相遇后，则15x+30x=30+3，③若是甲到达B地前，而乙到达A地后按原路返回时，则15x﹣30（x﹣1）=3，分别解方程即可．
练习册系列答案
相关题目
