题目内容
【题目】认真阅读下列材料,然后完成解答:
(材料)
如图,已知平面直角坐标系中两点A(x1,y1)、B(x2,y2),如何求A、B两点间的的距离|AB|的值?
过点A向y轴作垂线AN1、过点B向x轴作垂线BM2,垂足分别为N1(0,y1)和M2(x2,0),直线AN1和BM2相交于点Q.
在Rt△AQB中,|AB|2= |AQ|2+ |BQ|2
为了计算AQ和BQ,过点A向x轴作垂线,垂足为M1(x1,0);过点B向y轴作垂线,垂足为N2(0,y2),于是有|AQ|=|M1M2|=|x3-x1|,|BQ|=|N1N2|=|y2-y1|.
所以,|AB|2=![]() .
.
由此得到A(x1,y1)、B(x2,y2)两点间的距离公式:![]() .
.
根据定义:两点之间线段的长度,叫做这两点之间的距离.
因此,线段AB的长度计算公式为![]() .
.
(问题)
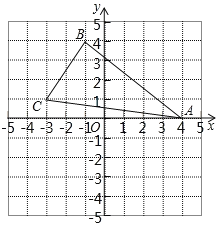
(1)平面直角坐标系中有两点A(0,1)、B(2,3),求线段AB的长;
(2)![]() 表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
(3)如图,在x轴上有一点P(x,0),试求PA+PB的最小值.

【答案】(1)AB=![]() ;(2)(-2,0);(3)
;(2)(-2,0);(3)![]() .
.
【解析】
(1)利用两点间的距离公式![]() 进行计算即可;
进行计算即可;
(2)由点M坐标为(a,b),可将MN变化为![]() ,可得点N坐标为(-2,0);
,可得点N坐标为(-2,0);
(3)作点A关于x轴的对称点A′,连接BA′,直线BA′于x轴的交点即为所求的点P,AP=A′P,A′B=A′P+BP=PA+PB,根据两点之间,线段最短,可得A′B等于PA+PB的最小值;
解:
(1)将点A(0,1)、B(2,3)代入![]() 得,
得,
![]() =
=![]() =
=![]() =
=![]() ;
;
∴AB的长为![]() ;
;
(2)由题可知,![]() ,点M坐标为(a,b),
,点M坐标为(a,b),
∴![]() ,
,
∴点N坐标为(-2,0);
(3)如图:作点A关于x轴的对称点A′(0,-1),连接A′B,交x轴于点P,可得,AP=A′P,A′B=A′P+BP=PA+PB,
根据两点之间,线段最短,可得A′B等于PA+PB的最小值.
![]() =
=![]() =
=![]() =
=![]() ;
;