题目内容
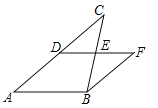
【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;
(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
试题解析:(1)连接DB,CF,

∵DE是△ABC的中位线,∴CE=BE,∵EF=ED,∴四边形CDBF是平行四边形,∴CD=BF;
(2)∵四边形CDBF是平行四边形,∴CD∥FB,∴AD∥BF,∵DE是△ABC的中位线,∴DE∥AB,∴DF∥AB,∴四边形ABFD是平行四边形.

练习册系列答案
相关题目