Question

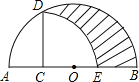
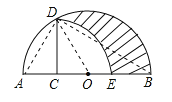
【题目】如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧交AB于E点，若AB＝4，则图中阴影部分的面积是（　　）

A. B. C. D.

Answer 1

【答案】A

【解析】分析：根据图形可得：阴影部分的面积=S半圆﹣（S扇形OAD﹣S△CDO+S扇形CDE），根据扇形面积公式、三角形面积公式计算即可．

详解：连接AD，OD，BD．

∵AB为半圆O的直径，∴∠ADB=90°，又CD⊥AB，∴△ACD∽△CDB，∴=，即=，∴CD=，又OC=1，∴∠COD=60°，∴S扇形OAD==π，S△CDO=×CO×CD=，∴S扇形OAD﹣S△CDO═π﹣，S扇形CDE==π，∴阴影部分的面积=S半圆﹣（S扇形OAD﹣S△CDO+S扇形CDE）=π+．

故选A．