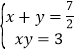Question

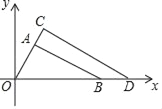
【题目】如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，∠OCD=90°，∠AOB=60°，若点B的坐标是（6，0），则点C的坐标是____．

Answer 1

【答案】（2，2）．

【解析】

分别过A、C作AE⊥OB，CF⊥OB，根据直角三角形的性质得到∠OCF=30°，根据位似图形的性质求出点D的坐标，解直角三角形求出FO,CF即可.

分别过A、C作AE⊥OB，CF⊥OB，

∵∠OCD=90°，∠AOB=60°，

∴∠ABO=∠CDO=30°，∠OCF=30°，

∵△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，点B的坐标是（6，0），

∴D（8，0），则DO=8，

故OC=4，

则FO=2，

故点C的坐标是：

故答案为：