题目内容
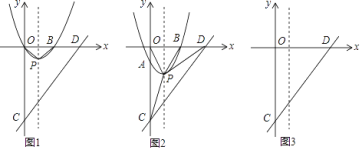
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
【答案】(1)(2,0);等腰直角三角形;(2)(i)![]() 或
或![]() ;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
【解析】
(1)根据自变量与函数值得对应关系,可得B点坐标,根据配方法,可得顶点坐标,根据勾股定理及勾股定理的逆定理,可得答案;
(2)根据自变量与函数值得对应关系,可得C,D,M点坐标,根据平移规律,可得P点坐标,根据平行于y轴的直线上两点间的距离较大的纵坐标减较小的纵坐标,可得PM的长,(i)根据面积的关系,可得关于m的方程,根据解方程,可得到顶点坐标;(ii)根据三角形的面积,可得答案.
(1)当y=0时,x2﹣2x=0,解得x=0(舍)或x=2,即B点坐标为(2,0),
∵抛物线y=x2﹣2x=(x﹣1)2﹣1,
∴P点坐标为(1,﹣1),由勾股定理,得
OP2=(2﹣1)2+12=2,
∴OP2+BP2=OB2 , OP=BP,
∴△OBP是等腰直角三角形,
(2)解:∵直线y=x﹣4与y轴交于点C,与x轴交于点D,
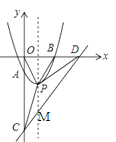
∴C(0,﹣4),D(4,0),当x=1时,y=﹣3,即M(1,﹣3),
抛物线向下平移m个单位长度,解析式为y=(x﹣1)2﹣(1+m),P(1,﹣1﹣m),
∴![]()
S△PCD=S△PMC+S△PMD= ![]() PM|xP﹣xC|=
PM|xP﹣xC|= ![]() |m﹣2|×4=2|m﹣2|,
|m﹣2|×4=2|m﹣2|,
(i)S△POC= ![]() AC|xP|=
AC|xP|= ![]() ×4×1=2,
×4×1=2,
∵S△PCD= ![]() S△POC,
S△POC,
∴S△PCD=2|m﹣2|=2![]() ,
,
解得m=2+ ![]() 或m=2﹣
或m=2﹣![]() ,
,
∴![]() 或
或![]() ;
;
(ii)![]()
①当m≥2时,S△PCD=2|m﹣2|=2m﹣4,S△POD=2|m+1|=2m+2,
∴S△POD﹣S△PCD=6
②当﹣1≤m<2时,S△PCD=2|m﹣2=4﹣2m,S△POD=2|m+1|=2m+2,
∴S△POD+S△PCD=6
③当m<﹣1时,S△PCD=2|m﹣2|=4﹣2m,S△POD=2|m+1|=2﹣2m,
∴S△POD﹣S△PCD=6,
综上所述:当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案