题目内容
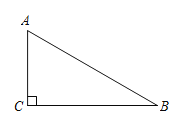
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,沿直线
边上一点,沿直线![]() 翻折
翻折![]() ,点
,点![]() 落在点
落在点![]() 处,如果
处,如果![]() ,那么
,那么![]() 的长为__________.
的长为__________.
【答案】2![]() -2
-2
【解析】
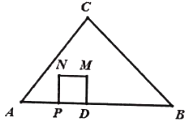
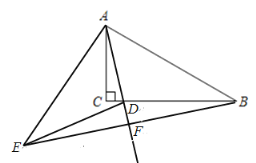
先根据题意补全图形,并求出AC,BC的长.再根据折叠的性质可推出△ABF为等腰直角三角形,从而得出BF的长,设CD=x,则BD=![]() -x,再证明△ACD∽△BFD,得出
-x,再证明△ACD∽△BFD,得出![]() ,从而可用含x的式子表示出DF的长,又在Rt△BDF中,根据勾股定理可得出关于x的方程,解出x,从而可得出结果.
,从而可用含x的式子表示出DF的长,又在Rt△BDF中,根据勾股定理可得出关于x的方程,解出x,从而可得出结果.
解:在Rt△ACB中,∠C=90°,∠BAC=60°,BC=![]() ,
,
∴AC=1,AB=2.
由折叠的性质可得AF⊥BE,
又∠ABF=45°,∴∠BAF=90°-45°=45°,
∴AF=BF,∴![]() BF=AB,∴BF=
BF=AB,∴BF=![]() .
.
设CD=x,则BD=![]() -x,
-x,
∵∠C=∠BFD=90°,∠ADC=∠BDF,
∴△ACD∽△BFD,
∴![]() ,即
,即![]() ,
,
∴DF=![]() .
.
在Rt△BDF中,BD2=DF2+BF2,
∴(![]() -x)2=(
-x)2=(![]() )2+(
)2+(![]() )2,
)2,
整理得,x2+2![]() x-1=0,
x-1=0,
解得x=2-![]() ,或x=-2-
,或x=-2-![]() (舍去),
(舍去),
即CD=2-![]() ,∴BD=
,∴BD=![]() -x=2
-x=2![]() -2.
-2.
故答案为:2![]() -2.
-2.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目