题目内容
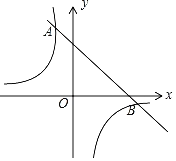
【题目】反比例函数y= ![]() (x>0) 的图像经过矩形ABCD的顶点A、C,AC的垂直平分线分别交AB、CD于点P、Q;己知点B坐标为(1,2),矩形ABCD的面积为8.
(x>0) 的图像经过矩形ABCD的顶点A、C,AC的垂直平分线分别交AB、CD于点P、Q;己知点B坐标为(1,2),矩形ABCD的面积为8.
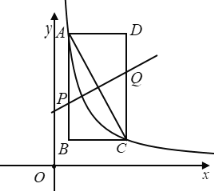
(1)求k的值;
(2)求直线PQ的解析式;
(3)连接PC、AQ,判断四边形APC Q的形状,并证明.
【答案】(1)k=6;(2)y=![]() x+3;(3)菱形,证明见解析.
x+3;(3)菱形,证明见解析.
【解析】
(1)设![]() ,根据矩形面积等于8得出
,根据矩形面积等于8得出![]() ,再由
,再由![]() 得出
得出![]() 的坐标,根据
的坐标,根据![]() 均在反比例图象上建立等量关系从而解方程组即可;
均在反比例图象上建立等量关系从而解方程组即可;
(2)设![]() 与
与![]() 相交于点
相交于点![]() ,根据
,根据![]() 算出
算出![]() 长度,从而算出
长度,从而算出![]() 点,再根据
点,再根据![]() 得出
得出![]() 的长度,从而算出
的长度,从而算出![]() 点,最后算出解析式;
点,最后算出解析式;
(3)由(2)知![]() ,从而得出四边形
,从而得出四边形![]() 是平行四边形,再根据垂直平分线性质得出
是平行四边形,再根据垂直平分线性质得出![]() ,从而得出四边形
,从而得出四边形![]() 是菱形.
是菱形.
(1)解:![]() 由矩形面积可知,
由矩形面积可知,![]()
∴A点的坐标为![]() ,点C的坐标为
,点C的坐标为![]()
由点A和点B在反比例函数图象上即可得到,![]()
∴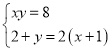 解得
解得![]()
∴![]()
(2)解:设![]() 与
与![]() 相交于点
相交于点![]() ,如图:
,如图:
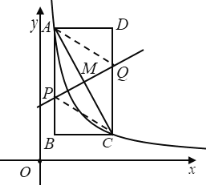
根据(1)可得,![]()
∴![]()
∵![]() 垂直平分
垂直平分![]()
∴![]() 得:
得:![]()
解得,![]() , 即点
, 即点![]() 的坐标为(1,
的坐标为(1,![]() )
)
又∵![]()
∴![]()
∴![]() ,可得点
,可得点![]() 的坐标为(3,
的坐标为(3,![]() )
)
设![]() 的解析式为
的解析式为![]() 则有:
则有:
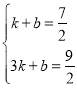 解得
解得![]()
∴![]() 的解析式为
的解析式为![]()
(3)连接![]() 如图:
如图:

由(2)知![]() ∵
∵![]()
∴四边形![]() 平行四边形
平行四边形
由线段垂直平分线的性质可得: ![]()
∴平行四边形![]() 为菱形.
为菱形.

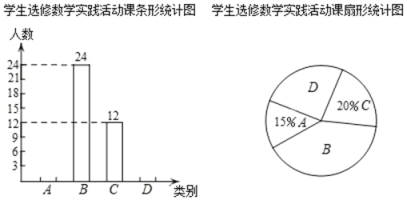
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.