��Ŀ����
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ����D�ڱ�AB�ϣ���
����D�ڱ�AB�ϣ���![]() ������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������
������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������![]() �����P�˶���ʱ��Ϊ
�����P�˶���ʱ��Ϊ![]() �룬������
�룬������![]() ��
��![]() �ص����ֵ����Ϊ
�ص����ֵ����Ϊ![]() ��
��
��1���ú���![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��2������![]() ����
����![]() �ı���ʱ����
�ı���ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
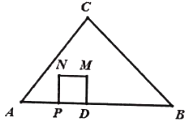
��4������P���߶�AD���˶�ʱ������N����CD�ĶԳƵ�![]() ����
����![]() ��
��![]() ��ijһ�����������ƽ��
��ijһ�����������ƽ��![]() �����ʱ����
�����ʱ����![]() ��ֵ��
��ֵ��
���𰸡���1����0![]() t
t![]() 3ʱPD=3-t����3��t
3ʱPD=3-t����3��t![]() 7ʱ��PD=t-3����2��
7ʱ��PD=t-3����2��![]() ��
��![]() ����3��
����3��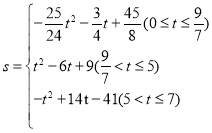 ����4��
����4��![]() ��
��![]() ��
��![]() ��
��
��������
��1����0��t��3ʱ��3��t��7ʱ���������ηֱ���⼴�ɣ�
��2����������������ͼ2�У�����N��AC��ʱ������ͼ3�У�����N��BC��ʱ������ƽ���߷��߶γɱ�������������⼴�ɣ�
��3�����������Σ�����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM������ͼ5��6�У���
ʱ���ص������������EFPDM������ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN������ͼ7�У���5��t��7ʱ���ص������������EFPDM���ֱ���⼴�ɣ�
��t��5ʱ���ص�������������PDMN������ͼ7�У���5��t��7ʱ���ص������������EFPDM���ֱ���⼴�ɣ�
��4�����������λ���ͼ�Σ�����ƽ���߷��߶γɱ��������������̼��ɽ�����⣮
�⣺��1����ͼ1�У���CD���AB��D��
�ߡ�B��45�㣬BC��4![]() ��
��
��CD�䣽BD�䣽4��
�֡�CD���AB��![]() ��
��
����Rt��ACD����
AD�䣽![]() ��
��
��AD��3��
��AD��AD�䣬
��D����D�غϣ�
��0��t��3ʱ��PD��3��t��
��3��t��7ʱ��PD��t��3��
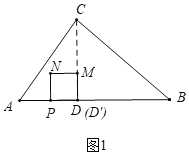
��2������ͼ2�У�����N��AC��ʱ��
��MN��AD��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
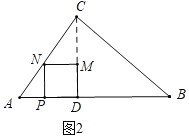
����ͼ3�У�����N��BC��ʱ��
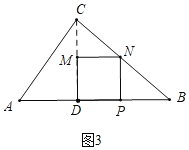
��MN��BD��
��![]() ��
��
��![]() ��
��
���t��5
��������������������t��ֵΪ![]() s��5s��
s��5s��
��3������ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
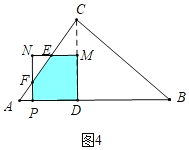
s��S������MDPN��S��NEF����3��t��2��![]()
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��s��t2��6t+9
��t��5ʱ���ص�������������PDMN��s��t2��6t+9
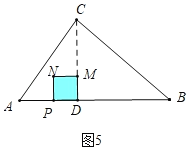
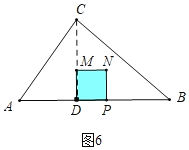
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��s��S������MNPD��S��EFN����t��3��2��![]() [��t��3������7��t��]2����t2+14t��41��
[��t��3������7��t��]2����t2+14t��41��

����������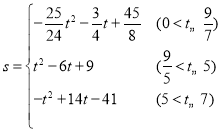 ��
��
��4����ͼ8�У�����N����������AE��ʱ����EK��BC��K��N��J��AB��J��
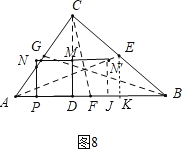
��JN���EK��
��![]() ��
��
����![]() ��
��
���t��1��
��ͼ9�У�����N����������BG��ʱ����GK��BC��K��N��J��/span>AB��J��
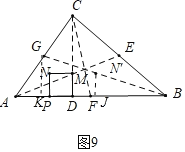
��N��J��GK��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��ͼ10�У�����N����������CF��ʱ��
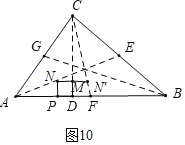
��MN���DF��
��![]() ��
��
��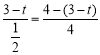 ��
��
���t��![]() ��
��
��������������������t��ֵΪ1s��![]() s��
s��![]() s��
s��