Question

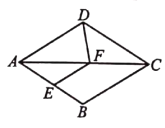
【题目】已知：如图，在菱形中，，．点为边上的一个动点（与点、不重合），，与边相交于点，联结交对角线于点．设，．

（1）求证：是等边三角形；

（2）求关于的函数解析式，并写出的取值范围；

（3）点是线段的中点，联结，当时，求的值．

Answer 1

【答案】（1）见解析；（2）y=（0＜x＜2）；（3）．

【解析】

（1）首先由△ABC是等边三角形，即可得AB=AC，求得∠ACF=∠B=60°，然后利由∠BAC=∠EAF=60°，可证明∠BAE=∠CAF，从而可证得△AEB≌△AFC，即可得AE=AF，证得△AEF是等边三角形；

（2）过点E作EH⊥AC于点H，过点F作FM⊥AC于点M，先用含x的代数式表示出HM，然后证明△EGH∽△FGM，得出，从而可用含x的代数式表示出HG，最后在Rt△EHG中，利用勾股定理可得出x，y之间的关系；

（3）先用含x的代数式表示出CG的长，然后证明△COE∽△CGF，得出，从而可得出关于x的方程，解出x的值即可．

（1）证明：∵四边形ABCD是菱形，
∴AB=BC=CD=AD，∠B=∠D=60°，
∴△ABC，△ACD都是等边三角形，
∴AB=AC，∠B=∠ACF=60°，
∵∠BAC=∠EAF=60°，
∴∠BAE=∠CAF，
∴△BAE≌△CAF（ASA），
∴AE=AF，又∠EAF=60°，

∴△AEF为等边三角形．

（2）解：过点E作EH⊥AC于点H，过点F作FM⊥AC于点M，

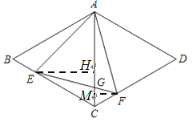
∵∠ECH=60°，∴CH=，EH=x，

∵∠FCM=60°，由（1）知，CF=BE=2-x，∴CM=（2-x），FM=（2-x），

∴HM=CH-CM=-（2-x）=x-1．

∵∠EHG=∠FMG=90°，∠EGH=∠FGM，

∴△EGH∽△FGM，∴，∴，

∴，∴HG=．

在Rt△EHG中，EG2=EH2+HG2，

∴y2=（x）2+[]2，∴y2=，∴y=（舍去负值），

故y关于x的解析式为y=（0＜x＜2）．

（3）解：如图，

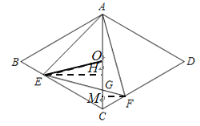
∵O为AC的中点，∴CO=AC=1．

∵EO=EG，EH⊥OC，∴OH=GH，∠EOG=∠EGO，∴∠CGF=∠EOG．

∵∠ECG=60°，EC=x，∴CH=，∴OH=GH=OC-CH=1-，∴OG=2OH=2-x，

∴CG=OC-OG=x-1．

∵∠CGF=∠EOC，∠ECO=∠GCF=60°，

∴△COE∽△CGF，

∴，∴，整理得x2=2，

∴x=（舍去负值），经检验x是原方程的解．

故x的值为．