ЬтФПФкШн
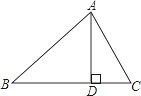
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЫљЪОЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌЕуDдкаББпABЩЯЃЌЕуEдкжБНЧБпBCЩЯЃЌШєЁЯCDEЃН45ЁуЃЌЧѓжЄЃКЁїACDЁзЁїBDEЃЎ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃЌдкОиаЮABCDжаЃЌABЃН4cmЃЌBCЃН10cmЃЌЕуEдкBCЩЯЃЌСЌНгAEЃЌЙ§ЕуEзїEFЁЭAEНЛCDЃЈЛђCDЕФбгГЄЯпЃЉгкЕуFЃЎ
ЂйШєBEЃКECЃН1ЃК9ЃЌЧѓCFЕФГЄЃЛ
ЂкШєЕуFЧЁКУгыЕуDжиКЯЃЌЧыдкБИгУЭМЩЯЛГіЭМаЮЃЌВЂЧѓBEЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйCFЃН![]() ЃЛЂкBEЕФГЄЮЊ2cmЛђ8cm
ЃЛЂкBEЕФГЄЮЊ2cmЛђ8cm
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕШбќжБНЧШ§НЧаЮаджЪжЊЁЯA=ЁЯB=45ЁуЁЂЁЯACD+ЁЯADC=135ЁуЃЌИљОнЁЯCDE=45ЁужЊЁЯADC+ЁЯBDE=135ЁуЃЌОнДЫЕУГіЁЯBDE=ЁЯACDЃЌДгЖјЕУжЄЃЛ
ЃЈ2ЃЉЂйгЩОиаЮЕФаджЪМАEFЁЭAEжЊЁЯBAE+ЁЯAEB=90ЁуЁЂЁЯCEF+ЁЯBEA=90ЁуЃЌЕУГіЁЯBAE=ЁЯCEFЃЌМДПЩжЄЁїBAEЁзЁїCEFЕУ![]() =
=![]() ЃЌОнДЫМЦЫуПЩЕУЃЛ
ЃЌОнДЫМЦЫуПЩЕУЃЛ
ЂкЩшBE=xcmЃЌгЩЂйЕУЁїBAEЁзЁїCEFЃЌОнДЫжЊ![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌНтжЎМДПЩ.
ЃЌНтжЎМДПЩ.
НтЃКЃЈ1ЃЉЁпдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌ
ЁрЁЯA=ЁЯB=45ЁуЃЌ
ЁрЁЯACD+ЁЯADC=135ЁуЃЌ
ЁпЁЯCDE=45ЁуЃЌ
ЁрЁЯADC+ЁЯBDE=135ЁуЃЌ
ЁрЁЯBDE=ЁЯACDЃЌ
ЁрЁїACDЁзЁїBDEЃЛ
ЃЈ2ЃЉЂйЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯB=ЁЯC=90ЁуЃЌ
ЁрЁЯBAE+ЁЯAEB=90ЁуЃЌ
ЁпЁЯAEF=90ЁуЃЌ
ЁрЁЯCEF+ЁЯBEA=90ЁуЃЌ
ЁрЁЯBAE=ЁЯCEFЃЌ
ЁрЁїBAEЁзЁїCEFЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁпBEЃКEC=1ЃК9ЃЌ
ЁрBE=![]() BC=1cmЃЌCE=9cmЃЌ
BC=1cmЃЌCE=9cmЃЌ
Ёр![]() =
=![]() ЃЌCF=
ЃЌCF=![]() ЃЛ
ЃЛ
ЂкШчЭМЫљЪОЃЌЩшBE=xcmЃЌ
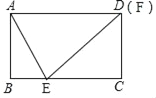
гЩЂйЕУЁїBAEЁзЁїCEFЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
ећРэЃЌЕУЃКx2Љ10x+16=0ЃЌ
НтЕУЃКx1=2ЃЌx2=8ЃЌ
ЫљвдBEЕФГЄЮЊ2cmЛђ8cmЃЎ

 ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ