题目内容
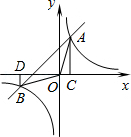
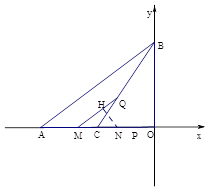
如图,平面直角坐标系中O为坐标原点,直线 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;

(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;
(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒
 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
(1)y= x+6 (2)
x+6 (2)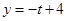 (0<t<4) (3)
(0<t<4) (3) 或
或 时,直线QM与⊙N相切.
时,直线QM与⊙N相切.
 x+6 (2)
x+6 (2)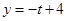 (0<t<4) (3)
(0<t<4) (3) 或
或 时,直线QM与⊙N相切.
时,直线QM与⊙N相切.试题分析:(1)∵
 ∴x=0时,y=6;y=0时,x=﹣8, ∴B(0,6) A(﹣8,0) ∵C为OA中点,∴C(﹣4,0)
∴x=0时,y=6;y=0时,x=﹣8, ∴B(0,6) A(﹣8,0) ∵C为OA中点,∴C(﹣4,0) 设BC:
 ∴﹣4k+b=0, b=6,∴k=
∴﹣4k+b=0, b=6,∴k= ∴y=
∴y= x+6
x+6 (2)∵QM∥AB ∴
 ∴
∴
∴CM=t,∴
 ,∴
,∴ ,∵
,∵
∴0<t<4<时,PM=
 ∴
∴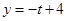 (0<t<4)
(0<t<4)(3)过N点作NH⊥MQ交直线MQ于H点.
∵N为PC的中点,∴
 ,MN=
,MN=
∵MQ∥AB
∴∠QMC=∠BAO
∴sin∠QMC=sin∠BAO=

∴NH=2×
 =
=
∵PC=

∴
 =2×
=2× =
= ,解得,
,解得, 或
或
综上,
 或
或 时,直线QM与⊙N相切.
时,直线QM与⊙N相切.点评:本题考查函数解析式和圆与圆的位置关系,要求考生会用待定系数法求一次函数的解析式,及判断圆与圆的位置关系的方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与双曲线
与双曲线 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.

 x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
 的图象与x轴,y轴交于A,B两点,与反比例函数
的图象与x轴,y轴交于A,B两点,与反比例函数 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:

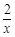 的图象交于A、B两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是
的图象交于A、B两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是