题目内容
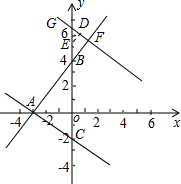
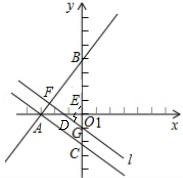
如图,直线y= x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
(1)求直线AC的解析式;
(2)直线l在平移过程中,请直接写出△BOF为等腰三角形时点F的坐标;
(3)直线l在平移过程中,设点E到直线l的距离为d,求d与t的函数关系.
 x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.(1)求直线AC的解析式;
(2)直线l在平移过程中,请直接写出△BOF为等腰三角形时点F的坐标;
(3)直线l在平移过程中,设点E到直线l的距离为d,求d与t的函数关系.

(1)y=﹣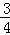 x﹣
x﹣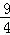 (2)F1(
(2)F1(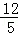 ,
,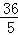 )、F2(﹣
)、F2(﹣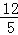 ,
,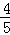 )、F3.(﹣
)、F3.(﹣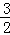 ,2)
,2)
(3)d=﹣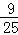 t+
t+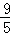 d=
d=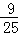 t﹣
t﹣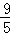
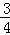 x﹣
x﹣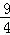 (2)F1(
(2)F1(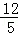 ,
,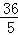 )、F2(﹣
)、F2(﹣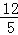 ,
,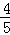 )、F3.(﹣
)、F3.(﹣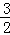 ,2)
,2)(3)d=﹣
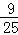 t+
t+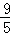 d=
d=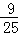 t﹣
t﹣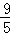
试题分析:(1)∵y=
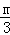 x+m交x轴负半轴于点A、交y轴正半轴于点B,
x+m交x轴负半轴于点A、交y轴正半轴于点B,∴B(0,m)、A(﹣3,0).
∵AB=5,
∴m2+32=52,
解得m=±4.
∵m>0,
∴m=4.
∴B(0,4).
∴OB=4.
∵直线AC⊥AB交y轴于点C,易得△BOA∽△AOC,
∴
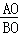 =
=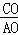 .
.∴CO=
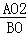 =
=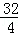 =
=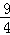 .
.∵点C在y轴负半轴上,
∴C(0,﹣
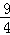 ).
).设直线AC解析式为y=kx+b,
∵A(﹣3,0),C(0,﹣
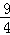 ),
),∴
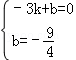 ,
,解得
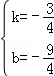 ,
,∴y=﹣
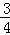 x﹣
x﹣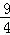 ;
;(2)F1(
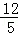 ,
,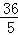 )、F2(﹣
)、F2(﹣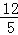 ,
,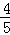 )、F3.(﹣
)、F3.(﹣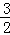 ,2);
,2);(3)分两种情况:第一种情况:当0≤t≤5时,
如图,作ED⊥FG于D,则ED=d.
由题意,FG∥AC,
∴
 =
=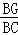 ,
,∵AF=t,AB=5,
∴BF=5﹣t.
∵B(0,4),
∴BC=4+
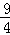 =
=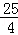 .
.∴
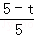 =
= .
.∴BG=
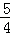 (5﹣t).
(5﹣t).∵OE=0.8t,OB=4,
∴BE=4﹣0.8t.
∴EG=
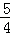 (5﹣t)﹣(4﹣0.8t)=
(5﹣t)﹣(4﹣0.8t)=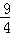 ﹣
﹣ t.
t.∵FG⊥AB,ED⊥FG,
∴∠GDE=∠GFB=90°.
∴ED∥AB.
∴
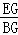 =
=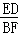 .
.∴
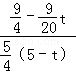 =
=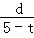 .
.∴d=﹣
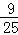 t+
t+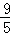 .
.第二种情况:当t>5时,
如图(2),
作ED⊥FG于D,则ED=d,
则题意,FG∥AC,
∴
 =
=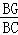 .
.∵AF=t,AB=5,
∴BF=t﹣5.
∵B(0,4),C(0,﹣
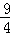 ),
),∴BC=4+
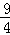 =
=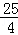 .
.∴
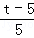 =
= .
.∴BG=
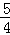 (t﹣5).
(t﹣5).∵OE=0.8t,OB=4,
∴BE=0.8t﹣4,EG=
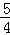 (t﹣5)﹣(0.8t﹣4),
(t﹣5)﹣(0.8t﹣4),=
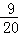 t﹣
t﹣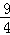 .
.∵FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,
∴ED∥AB.
∴
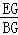 =
=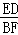 .
.∴
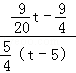 =
=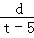 .
.∴d=
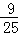 t﹣
t﹣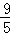 .
.
点评:此题考查了一次函数的综合;解题的关键是求出各点的坐标,再用各点的坐标求出解析式,注意(3)中分两种情况进行讨论,不要漏掉.

练习册系列答案
相关题目
 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;
 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
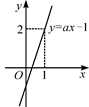
 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 的图象相交于C点.
的图象相交于C点.