题目内容
【题目】如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
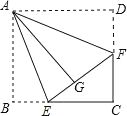
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
【答案】(1)见解析;(2)AB=![]() .
.
【解析】
(1)由题意得,∠BAE=∠EAG,∠DAF=∠FAG,于是得到∠BAD=2∠EAF=90°,推出四边形ABCD是矩形,根据正方形的判定定理即可得到结论;
(2)根据EC=FC=1,得到BE=DF,根据勾股定理得到EF的长,即可求解.
(1)由折叠性质知:∠BAE=∠EAG,∠DAF=∠FAG,
∵∠EAF=45°,
∴∠BAD=2∠EAF=2![]() 45°=90°,
45°=90°,
又∵∠B=∠D=90°,
∴四边形ABCD是矩形,
由折叠性质知:AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)∵EC=FC=1,
∴BE=DF,EF=![]() ,
,
∵EF=EG+GF=BE+DF,
∴BE=DF=![]() EF=
EF=![]() ,
,
∴AB=BC=BE+EC=![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;
(3)结合函数的图象,写出该函数的一条性质:_____________________________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是___________________.
有2个实数根,则t的取值范围是___________________.