Question

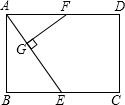
如图，在矩形ABCD中，点E在AD边上，AE＞DE，BE=BC，点O是线段CE的中点．
（1）试说明CE平分∠BED；
（2）若AB=3，BC=5，求BO的长；
（3）延长BO交直线AD于点F，连接CF，画出图形，试说明四边形BCFE是菱形．

Answer 1

（1）∵四边形ABCD是矩形，
∴AD∥BC，
∴∠BCE=∠DEC，
又∵BE=BC，∴∠BCE=∠BEC．
∴∠BEC=∠DEC，
∴CE平分∠BED；

（2）在Rt△BAE中，AB=3，BE=BC=5，
有勾股定理得：AE=4，
在Rt△CDE中，CD=3，DE=1，
有勾股定理得：EC=

10

，
在Rt△BOC中，BC=5，CO=

10

2

，
由勾股定理得：BO=

BC2-CO2

=

3 10

2

，

（3）如图所示：
∵FE∥CB，
∴∠EFO=∠COB，
∵BE=BC，BO⊥CE，
∴EO=CO，
在△FEO和△BCO中，

∠EFO=∠OBC ∠EOF=∠COB EO=CO

，
∴△FEO≌△BCO（AAS），
∴EF=BC，
∴四边形EFCB是平行四边形，
∵EC⊥BF，
∴四边形EFCB是菱形．