Question

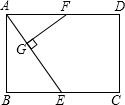
矩形ABCD中，E、F分别是BC、AD的中点，FG⊥AE于G，AB=6，AE=2

13

，BC=8，求FG的长．

Answer 1

连接EF，在梯形AECD中，EC=

1

2

BC=4，CD=AB=6．
∴S_梯形AECD=

1

2

(4+8)×6=36．
又S_梯形AECD=S_矩形FECD+S_△AEF=EC×CD+

1

2

×AE×FG．
即4×6+

1

2

×2

13

×FG=36．
∴FG=

12

13

13

．