题目内容
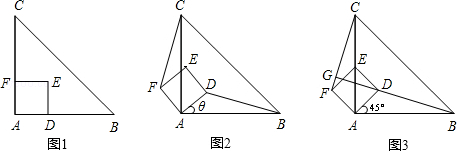
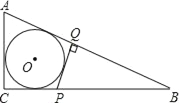
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设⊙O的半径是R,PE=PF=x,BQ=y,连接OD,OG,OF,OE,得出正方形CDOE和OGQF,推出OD=CD=CE=OE=GQ=QF=R,求出y=2R,x=![]() R,根据锐角三角函数值求出即可.
R,根据锐角三角函数值求出即可.
解:

设⊙O的半径是R,PE=PF=x,BQ=y,
连接OD,OG,OF,OE,
∵⊙O内切于Rt△ABC,
∴∠ODC=∠OEC=90°=∠C,AD=AG,
∵OD=OE,
∴四边形CDOE是正方形,
∴OD=CD=CE=OE=R,
同理OG=GQ=FQ=OF=R,
则PQ=CP,AC=AQ,
∵PQ⊥AB,∠C=90°,
∴∠C=∠PQB=90°,
∵∠B=∠B,
∴△BQP∽△BCA,
![]()
根据BG=BE得:y+R=2y-R,
解得:y=2R,
在Rt△PQB中,由勾股定理得:PQ2+BQ2=BP2,
即(2R)2+(R+x)2=(4R-R-x)2,
解得:![]() ,
,
即PQ=![]() ,BQ=2R.
,BQ=2R.
tanB=![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目