Question

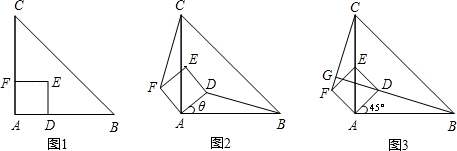
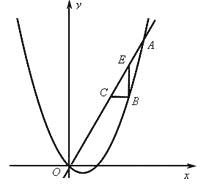
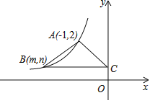
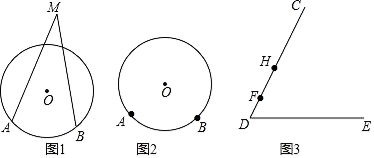
【题目】已知：如图，在△ABC中，点D在边AB上，点E在线段CD上，且∠ACD=∠B=∠BAE.

（1）求证：；

（2）当点E为CD中点时，求证：.

Answer 1

【答案】（1）证明见解析，（2）证明见解析..

【解析】

（1）欲证明，只要证明△AED∽△BAC即可解决问题；

（2）由△DAE∽△DCA，推出，由DE=EC，可得，推出，再证明AD2=ADAB即可解决问题；

（1）∵∠ACD=∠B=∠BAE，∠BAC=∠BAE+∠CAE，∠AED=∠ACD+∠CAE，

∴∠AED=△BAC，

∵∠DAE=∠B，

∴△AED∽△BAC，

∴．

（2）∵∠ADE=∠CDA，∠DAE=∠ACD，

∴△DAE∽△DCA，

∴，

∵DE=EC，

∴，

∴，

∵∠DAC=∠BAC，∠ACD=∠B，

∴△ACD∽△ABC，

∴AC2=ADAB，

∴．