题目内容
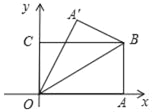
【题目】如图,在平面直角坐标系中,将矩形OABC沿着OB对折,使点A落在点A'处,点B的坐标(8,4),则点A'的坐标是( )
A. (4,![]() ) B. (
) B. (![]() ,
,![]() )
)
C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
【答案】B
【解析】
设出![]() 点的坐标,先根据翻折变换的性质得出
点的坐标,先根据翻折变换的性质得出![]() 的面积,作
的面积,作![]() E ⊥x轴于E,交DE于F,根据BC//x轴可知
E ⊥x轴于E,交DE于F,根据BC//x轴可知![]() E ⊥BC,再由BD的值及三角形的面积公式可求出
E ⊥BC,再由BD的值及三角形的面积公式可求出![]() 的长,B点坐标,用待定是法求出过O、D两点的一次函数的解析式,把
的长,B点坐标,用待定是法求出过O、D两点的一次函数的解析式,把![]() 点的坐代入函数解析式即可得到答案.
点的坐代入函数解析式即可得到答案.
解:![]() BC//AO,
BC//AO,![]() ∠BOA=∠OBC ,
∠BOA=∠OBC ,
根据翻折不变性得, ∠![]() =∠BOA,
=∠BOA,
![]() ∠OBC=∠
∠OBC=∠![]() ,
,
![]() DO=DB.
DO=DB.
设DO=DB=xcm,则CD=(8-x)cm,
又![]() OC=4,
OC=4,![]() +
+![]() =
=![]() ,
,
解得x=5. ![]() BD=5 ,
BD=5 ,
![]()
![]() =
=![]() =10;
=10;
设![]() (a,4+b),作
(a,4+b),作![]() E⊥x轴于E, 交DE于F,如下图所示:
E⊥x轴于E, 交DE于F,如下图所示:
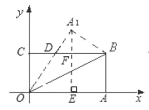
![]() BC//x轴,
BC//x轴,![]()
![]() E⊥BC ,
E⊥BC ,
![]()
![]() =
=![]() =
=![]() =16,
=16,![]() =10,
=10,
![]()
![]() =
=![]() =
=![]() =6
=6
解得![]() =6
=6
![]()
![]() 的纵坐标为
的纵坐标为![]()
![]() BD=5,B(8,4)
BD=5,B(8,4)
![]() D点坐标为(3,4),
D点坐标为(3,4),
![]() 过OD两点直线解析式为y=
过OD两点直线解析式为y=![]() ,
,
把![]() 点的坐标(a,
点的坐标(a,![]() )代入得
)代入得![]() ,
,
解得a=![]()
![]()
![]() 点的坐标为(
点的坐标为(![]() ,
,![]() )
)
故选:B.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目