题目内容
如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4)+y轴交与点C.
(1)求抛物线的解析式;
(2)求S△AOB;
(3)求
的值;
(4)判断点A是否在以BO为直径的圆上?并说明理由.
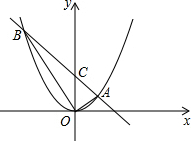
(1)求抛物线的解析式;
(2)求S△AOB;
(3)求
| BC |
| AC |
(4)判断点A是否在以BO为直径的圆上?并说明理由.

(1)∵抛物线y=ax2经过点B(-2,4),
∴4a=4,
∴a=1,
∴抛物线的解析式为y=x2;
(2)把点A(1,m)代入y=x2得m=1,
∴点A的坐标为(1,1),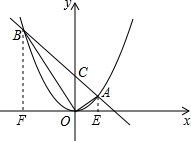
如图,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,
S△AOB=S梯形ABFE-S△AOE-S△BOF,
=
×(1+4)×(1+2)-
×1×1-
×2×4,
=
-
-4,
=3;
(3)∵AE⊥x轴,BF⊥x轴,OC⊥x轴,
∴AE∥BF∥OC,
∴
=
=2;
(4)∵直线y=kx+b经过A(1,1),B(-2,4),
∴
,
解得
,
∴直线AB的解析式为y=-x+2,
∵直线AB与y轴交与点C,
∴∠ACO=45°,
∵点A(1,1),
∴∠AOC=45°,
∴∠OAC=180°-45°-45°=90°,
∴点A在以BO为直径的圆上.
∴4a=4,
∴a=1,
∴抛物线的解析式为y=x2;
(2)把点A(1,m)代入y=x2得m=1,
∴点A的坐标为(1,1),

如图,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,
S△AOB=S梯形ABFE-S△AOE-S△BOF,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 15 |
| 2 |
| 1 |
| 2 |
=3;
(3)∵AE⊥x轴,BF⊥x轴,OC⊥x轴,
∴AE∥BF∥OC,
∴
| BC |
| AC |
| OF |
| OE |
(4)∵直线y=kx+b经过A(1,1),B(-2,4),
∴
|
解得
|
∴直线AB的解析式为y=-x+2,
∵直线AB与y轴交与点C,
∴∠ACO=45°,
∵点A(1,1),
∴∠AOC=45°,
∴∠OAC=180°-45°-45°=90°,
∴点A在以BO为直径的圆上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
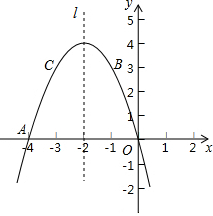
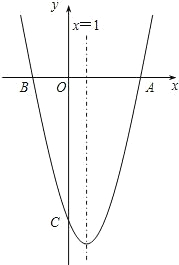 段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.
段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1. 点在直线BC上.
点在直线BC上.

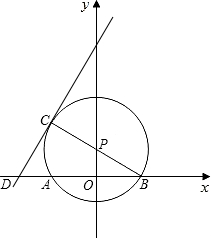 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为