题目内容
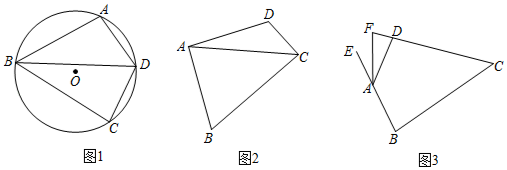
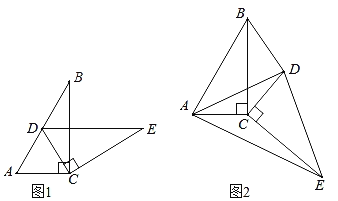
【题目】在矩形![]() 中,分别以
中,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.![]() 是
是![]() 边上一个动点(不与
边上一个动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 的反比例函数
的反比例函数![]()
![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,则
处,则![]() ________.
________.
【答案】![]()
【解析】
证明Rt△MEG∽Rt△BGF,则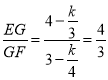 ,而EM:GB=EG:GF=4:3,求出GB,在Rt△GBF中,利用勾股定理即可求解.
,而EM:GB=EG:GF=4:3,求出GB,在Rt△GBF中,利用勾股定理即可求解.
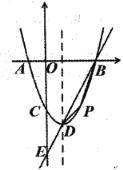
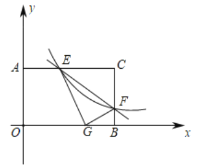
解:如图,过点E作EM⊥x轴于点M,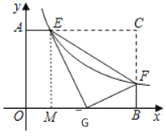
∵将△CEF沿EF对折后,C点恰好落在OB上的G点处,
∴∠EGF=∠C=90°,EC=EG,CF=GF,
∴∠MGE+∠FGB=90°,
而EM⊥OB,
∴∠MGE+∠MEG=90°,
∴∠MEG=∠FGB,
∴Rt△MEG∽Rt△BGF;
又∵EC=AC-AE=4-![]() ,CF=BC-BF=3-
,CF=BC-BF=3-![]() ,
,
∴EG=4-![]() ,GF=3-
,GF=3-![]() ,
,
∴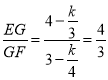 .
.
∵EM:GB=EG:GF=4:3,而EM=3,
∴GB=![]() ,
,
在Rt△GBF中,GF2=GB2+BF2,即(3-![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得k=![]() ,
,
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2020年春节,一场突如其来的新型冠状肺炎病毒疫情在武汉突发,为响应党中央号召,在“支援武汉,防控疫情”的过程中,某省计划组织1441名医护人员的“援汉”团队前往武汉进行支援,经过研究,决定租用当地租车公司一共62辆![]() 、
、![]() 两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 380元 |
| 20人 | 280元 |
注:载客量指的是每辆客车最多可载医护人员的人数.
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过19900元,一共有几种租车方案?哪种租车方案最省钱?