题目内容
【题目】在平面直角坐标系xOy中,过⊙T(半径为r)外一点P引它的一条切线,切点为Q,若0<PQ≤2r,则称点P为⊙T的伴随点.
(1)当⊙O的半径为1时,
①在点A(4,0),B(0,![]() ),C(1,
),C(1,![]() )中,⊙O的伴随点是 ;
)中,⊙O的伴随点是 ;
②点D在直线y=x+3上,且点D是⊙O的伴随点,求点D的横坐标d的取值范围;
(2)⊙M的圆心为M(m,0),半径为2,直线y=2x﹣2与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙M的伴随点,直接写出m的取值范围.
【答案】(1)①B,C;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①画出图形,利用勾股定理、圆的切线的性质求出切线长,再根据⊙O的伴随点的定义判断即可;
②如图2中,设点D的坐标为![]() ,先求出当切线长为
,先求出当切线长为![]() 时,OD的长,再利用两点之间的距离公式可求出d的值,由此即可得出答案;
时,OD的长,再利用两点之间的距离公式可求出d的值,由此即可得出答案;
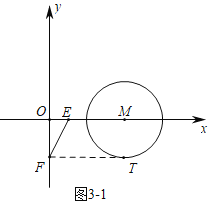
(2)求出临界位置时m的值即可判断:①如图3-1中,设FT是⊙M的切线,当![]() 时,求出此时m的值,再根据伴随点的定义,结合图象即可得;②如图3-2中,设ET是⊙M的切线,连接MT,则
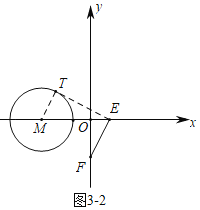
时,求出此时m的值,再根据伴随点的定义,结合图象即可得;②如图3-2中,设ET是⊙M的切线,连接MT,则![]() ,求出此时临界位置m的值,再根据伴随点的定义,如图3-3中,当⊙M在直线EF的左侧与EF相切时,设切点为T,连接MT,求出临界位置m的值,然后结合图象即可得.
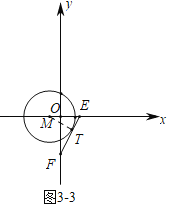
,求出此时临界位置m的值,再根据伴随点的定义,如图3-3中,当⊙M在直线EF的左侧与EF相切时,设切点为T,连接MT,求出临界位置m的值,然后结合图象即可得.
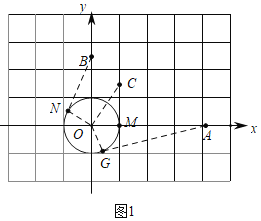
(1)①如图1,![]() 为⊙O的三条切线
为⊙O的三条切线
![]()
![]() ⊙O的半径为1
⊙O的半径为1
![]()
![]()
![]()
则切线AG的长为![]()
切线BN的长为![]()
切线CM的长为![]()
由⊙O的伴随点的定义得:点B,C是⊙O的伴随点
故答案为:B,C;
②如图2中,设点D的坐标为![]()
当过点D的切线长为![]() 时,
时,![]()
由两点之间的距离公式得:![]()
解得![]()
结合图象可知,点D的横坐标d的取值范围是![]() ;
;

(2)对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点E的坐标为
,则点E的坐标为![]()
当![]() 时,
时,![]() ,则点F的坐标为
,则点F的坐标为![]()
![]() ⊙M的半径为2,⊙M的圆心为
⊙M的半径为2,⊙M的圆心为![]()
![]() ,
,![]()
由题意,由以下两种情况:
如图3-1中,点M在点E的右侧
设FT是⊙M的切线
则有两个临界位置:![]() 和点E对应的切线长为0
和点E对应的切线长为0
当![]() 时,则
时,则![]()
当点E对应的切线长为0,即![]()
![]()
解得![]()
结合图象得,当![]() 时,线段EF上的所有点都是⊙M的伴随点
时,线段EF上的所有点都是⊙M的伴随点
②如图3-2和3-3中,点M在点E的左侧
则有如下两个临界位置:
如图3-2,设ET是⊙M的切线,连接MT,则![]()
当![]() 时,
时,![]()
此时![]()
解得![]()
如图3-3,当⊙M在直线EF的左侧与EF相切时,设切点为T,连接MT
∵![]()
∴![]()
∴![]()
∵EF是切线
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ,即
,即![]()
解得![]() ,即
,即![]()
解得![]()
结合图象得,当![]() 时,线段EF上的所有点都是⊙M的伴随点
时,线段EF上的所有点都是⊙M的伴随点
综上,m的取值范围是![]() 或
或![]() .
.