题目内容
【题目】如图,BD是∠ABC的角平分线,DE∥BC,交AB于点E,∠A=45°, ∠BDC=60°。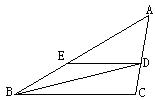
(1)求∠C的度数;
(2)求∠BED的度数.
【答案】
(1)
解:∵∠A=45°,∠BDC=60°,
∴∠ABD=∠BDC-∠A=15°.
∵BD是△ABC的角平分线,
∴∠DBC=∠ABD=15°,
∴∠ABC=30°,
∠C=180°-∠A-∠ABC=105°
(2)
∵DE∥BC,
∴∠AED=∠ABC=30°,
∠BED=180°-30°=150°
【解析】先根据三角形外角的性质求∠ABD,再根据角平分线的定义,可得∠DBC=∠ABD,利用三角形的内角和为180°求出∠C的度数;运用平行线的性质得∠BDE的度数,进而得出结论.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目