题目内容
【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC
(1)如图1,若α+β= ![]() ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
【答案】
(1)150
(2)
β-α=90°
理由:如图1,连接BD,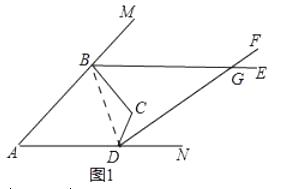
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=![]() ∠MBC,∠CDG=
∠MBC,∠CDG=![]() ∠NDC,
∠NDC,
∴∠CBG+∠CDG=![]() ∠MBC+∠NDC=
∠MBC+∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
在△BCD中,∠BDC+∠CBD=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴![]() (α+β)+180°-β+45°=180°,
(α+β)+180°-β+45°=180°,
∴β-α=90°,
(3)
平行,
理由:如图2,延长BC交DF于H,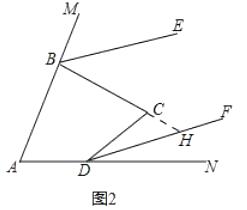
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=![]() ∠MBC,∠CDH=
∠MBC,∠CDH=![]() ∠NDC,
∠NDC,
∴∠CBE+∠CDH=![]() ∠MBC+
∠MBC+![]() ∠NDC=
∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=![]() (α+β),
(α+β),
∵α=β,
∴∠CBE+β-∠DHB=![]() (β+β)=β,
(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【解析】(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=150°,
∴∠MBC+∠NDC=150°.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案