题目内容
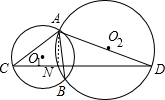如图，⊙O1与⊙O2相交于A、B两点，经过点B的一直线和两圆分别相交于点C和D，设此两圆的半径为R1，R2．求证：AC：AD=R1：R2．
分析：作AN⊥CD，垂足为点N，连接AB，根据相交圆的性质可知有AC．AB=AN.2R1，AB•AD=AN•2R2．进而得到所证结论．
解答：证明：作AN⊥CD，
垂足为点N，
连接AB，
有AC•AB=AN.2R1，①
AB•AD=AN•2R2．②
①÷②，得
=
，
∴AC：AD=R1：R2．
证明：作AN⊥CD，垂足为点N，
连接AB，
有AC•AB=AN.2R1，①
AB•AD=AN•2R2．②
①÷②，得
| AC |
| AD |
| R1 |
| R2 |
∴AC：AD=R1：R2．
点评：本题主要考查相交两圆的性质的知识点，根据圆内线段成比例，进而求证出所要结论，此题难度中等．
练习册系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=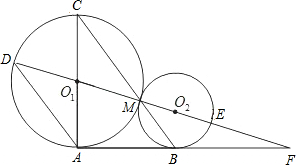
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
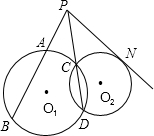如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
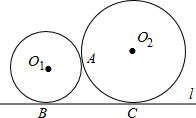已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
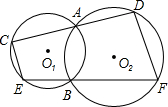已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．