题目内容
【题目】已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)若点G在点B的右边.试探索:EH![]() BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
BG的值是否为定值,若是,请求出定值;若不是,请说明理由.

(2)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数.
【答案】(1)EH![]() BG的值是定值4,(2)在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°
BG的值是定值4,(2)在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°
【解析】分析:![]() 根据垂直的定义得到∠GHE=90°,根据余角的性质得到
根据垂直的定义得到∠GHE=90°,根据余角的性质得到![]() 根据正方形的性质得到
根据正方形的性质得到![]() 判断出
判断出![]() 证明
证明![]() ≌
≌![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,根据线段的和差即可得到结论;
,根据线段的和差即可得到结论;
(2)分三种情况讨论:利用(1)得出![]() ≌
≌![]() ,再判断出△BHE是等腰直角三角形,即可得出结论.
,再判断出△BHE是等腰直角三角形,即可得出结论.
详解:(1)![]() 的值是定值,
的值是定值,
![]()
又![]() ,∴
,∴![]()
∵四边形ABCD与四边形DGEF都是正方形,
∴![]() ,∴
,∴![]()
在![]() 和
和![]() 中,
中,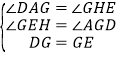 ,
,
∴![]() ≌
≌![]() (AAS);
(AAS);
∴![]()
又AG=AB+BG,AB=4,
∴EH=AB+BG,
∴EHBG=AB=4;
(2)(I)当点G在点B的左侧时,如图1,

同(2)①可证得:△DAG≌△GHE,
∴GH=DA=AB,EH=AG,
∴GB+BH=AG+GB,
∴BH=AG=EH,又![]() ,
,
∴△BHE是等腰直角三角形,
∴![]()
(II)如图2,当点G在点B的右侧时,
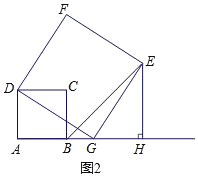
由(2)①证得:△DAG≌△GHE.
∴GH=DA=AB,EH=AG,
∴AB+BG=BG+GH,
∴AG=BH,又EH=AG
∴EH=HB,又![]() ,
,
∴△BHE是等腰直角三角形,
∴![]()
(III)当点G与点B重合时,
如图3,同理可证:△DAG≌△GHE,
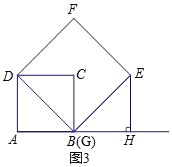
∴GH=DA=AB,EH=AG=AB,
∴△GHE(即△BHE)是等腰直角三角形,
∴![]()
综上,在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目