��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У��������¶��壺���ڵ�P��m��n��������Q��2��m��n��1������Ƶ�QΪ��P���������������磺�㣨��2��5����������������Ϊ��4��4����
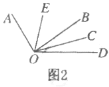
��1��ij������������������ǣ���1��3����������������Ϊ ��
��2������A�������ǣ�2��m��n��1������A����������ΪA1�㣬��A1����������ΪA2�㣬��A2����������ΪA3�㣬������A1�������� ����A2015�������� ��
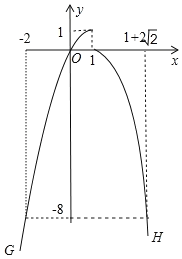
��3������y=��x2+2x��x��1����ͼ��ΪG��ͼ��G�����е��������������ͼ��H��ͼ��G��ͼ��H�����ͼ�μ�Ϊ��ͼ�����������㣨p��q������ͼ���������ƶ�ʱ����k��p��1+2![]() ����8��q��1����k��ȡֵ��Χ
����8��q��1����k��ȡֵ��Χ
���𰸡���1����3��4����2����m��n��2������4��m��n��2016����3����2��k��1
��������������(1)�������������Ϊ��m��n�������ݸ����Ķ���ó�2��m=��1��n��1=3���Ӷ��ó�m��n��ֵ���ó�������ꣻ(2)�����ݶ���ó�һ���ԵĹ��ɣ��Ӷ��ó��𰸣�(3)����������ó�����G�ͺ���H�ĺ�������ʽ��Ȼ������ƽ�Ƶ����ʵó�k��ȡֵ��Χ��
��⣺(1)�������������Ϊ��m��n�����������ġ��ĵ㡱�������ǣ���1��3����
��2��m=��1��n��1=3�� ��m=3��n=4�� ��������������3��4����
(2)��������A1��m��n��2����A2��m��2��n��3����A3��4��m��n��4����A4��m��2��n��5����A5��4��m��n��6������ �ɴ˹��ɿ�֪A2015��4��m��n��2016����
(3)����ͼ��������ͼ��G�Ľ���ʽΪy=��x2+2x����x��1����
ͼ��H�Ľ���ʽΪy=����x��1��2����x��1��
���ں���y=��x2+2x����y=��8ʱ����x2+2x=��8�� ���x=��2��8���������� ��x=��2��
��y=1ʱ����x2+2x=1�����x=1��
�����㣨p��q���ڡ�ͼ�Χ������ƶ�ʱ����k��p��1+2![]() ����8��q��1�� ����ͼ���֪����2��k��1��
����8��q��1�� ����ͼ���֪����2��k��1��