题目内容
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角![]() 为
为![]() ,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角
,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角![]() 为
为![]() ,点A、B、C三点在同一水平线上.
,点A、B、C三点在同一水平线上.
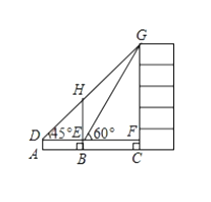
(1)求古树BH的高;
(2)求教学楼CG的高.
【答案】(1)8.5米;(2)![]() 米
米
【解析】
(1)利用等腰直角三角形的性质即可解决问题;
(2)作HJ⊥CG于G.则△HJG是等腰直角三角形,四边形EFJH是矩形,设GJ=EF=HJ=x.构建方程即可解决问题;
(1)由题意:四边形ABED是矩形,可得DE=AB=7米,AD=BE=1.5米,
在Rt△DEH中,∵∠HDE=45°,
∴HE=DE=7米,
∴BH=EH+BE=8.5米,
所以古树BH的高为8.5米;
(2)作HJ⊥CG于J.易证△HJG是等腰直角三角形,四边形EFJH是矩形,
∴JF=HE =7米,
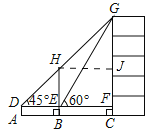
设HJ =x.则GJ=EF=HJ=x,
在Rt△EFG中,tan60°=![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (米);
(米);
所以教学楼CG的高为![]() 米.
米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目