ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΥφΉ≈…ζΜνΥ°ΤΫΒΡΧαΗΏΘ§»ΥΟ«Ε‘“ϊΥ°ΤΖ÷ ΒΡ–η«σ‘Ϋά¥‘ΫΗΏΘ§Ρ≥ΙΪΥΨΗυΨί –≥Γ–η«σ¥ζάμAΘ§BΝΫ÷÷–ΆΚ≈ΒΡΨΜΥ°ΤςΘ§ΟΩΧ®A–ΆΨΜΥ°Τς±»ΟΩΧ®B–ΆΨΜΥ°ΤςΫχΦέΕύ200‘ΣΘ§”Ο5Άρ‘ΣΙΚΫχA–ΆΨΜΥ°Τς”κ”Ο4.5Άρ‘ΣΙΚΫχB–ΆΨΜΥ°ΤςΒΡ ΐΝΩœύΒ»
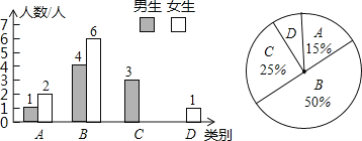
Θ®1Θ©«σΟΩΧ®A–ΆΓΔB–ΆΨΜΥ°ΤςΒΡΫχΦέΗς «Εύ…Ό‘ΣΘΩ
Θ®2Θ©ΗΟΙΪΥΨΦΤΜ°ΙΚΫχAΘ§BΝΫ÷÷–ΆΚ≈ΒΡΨΜΥ°ΤςΙ≤50Χ®Ϋχ–– ‘œζΘ§Τδ÷–A–ΆΨΜΥ°ΤςΈΣxΧ®Θ§ΙΚ¬ρΉ Ϋπ≤Μ≥§Ιΐ9.8Άρ‘ΣΘ§ ‘œζ ±A–ΆΨΜΥ°ΤςΟΩΧ® έΦέ2500‘ΣΘ§B–ΆΨΜΥ°ΤςΟΩΧ® έΦέ2180‘ΣΘ§ΙΪΥΨΨωΕ®¥”œζ έA–ΆΨΜΥ°ΤςΒΡάϊ»σ÷–Α¥ΟΩΧ®ΨηœΉa‘ΣΉςΈΣΙΪΥΨΑοΖωΤΕάߥε“ϊΥ°ΗΡ‘λΉ ΫπΘ°»τΙΪΥΨ έΆξ50Χ®ΨΜΥ°Τς≤ΔΨηœΉΖωΤΕΉ ΫπΚσΜώΒΟΒΡΉν¥σάϊ»σ≤ΜΒΆ”Ύ20200‘ΣΒΪ≤Μ≥§Ιΐ23000‘ΣΘ§«σaΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΩΧ®A–ΆΓΔB–ΆΨΜΥ°ΤςΒΡΫχΦέΖ÷±π «2000‘ΣΓΔ1800‘ΣΘΜΘ®2Θ©aΒΡ»Γ÷ΒΖΕΈß «20ΓήaΓή90Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΩ…“‘Ν–≥ωœύ”ΠΒΡΖ÷ ΫΖΫ≥ΧΘ§¥”ΕχΩ…“‘Ϋβ¥π±ΨΧβΘΜ
Θ®2Θ©ΗυΨίΧβ“βΩ…“‘«σΒΟxΒΡ»Γ÷ΒΖΕΈßΚΆάϊ»σ”κxΒΡΚ· ΐΙΊœΒ ΫΘ§»ΜΚσΗυΨί“Μ¥ΈΚ· ΐΒΡ–‘÷ Φ¥Ω…Ϋβ¥π±ΨΧβΘ°
Θ®1Θ©…ηΟΩΧ®A–ΆΒΡΫχΦέΈΣm‘ΣΘ§
![]() Θ§
Θ§
ΫβΒΟΘ§mΘΫ2000Θ§
Ψ≠Φλ―ιΘ§mΘΫ2000 «‘≠Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
Γύm©¹200ΘΫ1800Θ§
¥πΘΚΟΩΧ®A–ΆΓΔB–ΆΨΜΥ°ΤςΒΡΫχΦέΖ÷±π «2000‘ΣΓΔ1800‘ΣΘΜ
Θ®2Θ©2000x+1800Θ®50©¹xΘ©Γή98000Θ§
ΫβΒΟΘ§xΓή40Θ§
…ηΙΪΥΨ έΆξ50Χ®ΨΜΥ°Τς≤ΔΨηΩνΚσΜώΒΟΒΡάϊ»σΈΣw‘ΣΘ§
wΘΫΘ®2500©¹2000Θ©x+Θ®2180©¹1800Θ©Θ®50©¹xΘ©©¹axΘΫΘ®120©¹aΘ©x+19000Θ§
Β±aΓί120 ±Θ§wΓή19000≤ΜΚœΧβ“βΘ§
Β±aΘΦ120 ±Θ§120©¹aΘΦ0Θ§Β±xΘΫ40 ±Θ§w»ΓΒΟΉν¥σ÷ΒΘ§
Γύ20200Γή40Θ®120©¹aΘ©+19000Γή23000Θ§
ΫβΒΟΘ§20ΓήaΓή90Θ§
Φ¥aΒΡ»Γ÷ΒΖΕΈß «20ΓήaΓή90Θ°