题目内容
【题目】(1)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠ABC,射线BC上一点D.
求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等;

(2)在(1)的条件下,若∠ABC=60°,求等腰三角形△PBD顶角的度数.
【答案】(1)详见解析;(2)120°.
【解析】
(1)根据角平分线的性质、线段的垂直平分线的性质即可解决问题.
(2)根据已知,由角平分线定理可得∠PBD=![]() ∠ABC=30°,MN垂直平分线段BD,即PB=PD,∠PBD=∠PDB=30°,即可求得∠BPD的度数.
∠ABC=30°,MN垂直平分线段BD,即PB=PD,∠PBD=∠PDB=30°,即可求得∠BPD的度数.
解:(1)点P是∠ABC的平分线与线段BD的垂直平分线的交点,如图点P即为所求;
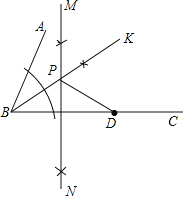
(2)∵∠ABC=60°,BP平分∠ABC,
∴∠PBD=![]() ∠ABC=30°,
∠ABC=30°,
∵MN垂直平分线段BD,
∴PB=PD,
∴∠PBD=∠PDB,
∴∠PBD=∠PDB=30°
∴∠BPD=180°﹣30°﹣30°=120°.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.






