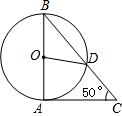
题目内容
已知:如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连接DE、BE,且∠C=∠BED.
(1)求证:AC是⊙O的切线;
(2)若OA=10,AD=16,求AC的长.

(1)求证:AC是⊙O的切线;
(2)若OA=10,AD=16,求AC的长.

(1)证明:∵∠BED=∠BAD,∠C=∠BED,
∴∠BAD=∠C.(1分)
∵OC⊥AD于点F,
∴∠BAD+∠AOC=90°.(2分)
∴∠C+∠AOC=90°.
∴∠OAC=90°.
∴OA⊥AC.
∴AC是⊙O的切线.(4分)
(2)∵OC⊥AD于点F,
∴AF=
AD=8.(5分)
在Rt△OAF中,OF=
=6,(6分)
∵∠AOF=∠AOC,∠OAF=∠C,
∴△OAF∽△OCA.(7分)
∴
=
.
即OC=
=
=
.(8分)
在Rt△OAC中,AC=
=
.(10分)
∴∠BAD=∠C.(1分)
∵OC⊥AD于点F,
∴∠BAD+∠AOC=90°.(2分)
∴∠C+∠AOC=90°.
∴∠OAC=90°.
∴OA⊥AC.
∴AC是⊙O的切线.(4分)
(2)∵OC⊥AD于点F,
∴AF=
| 1 |
| 2 |
在Rt△OAF中,OF=
| OA2-AF2 |
∵∠AOF=∠AOC,∠OAF=∠C,
∴△OAF∽△OCA.(7分)
∴
| OA |
| OC |
| OF |
| OA |
即OC=
| OA2 |
| OF |
| 100 |
| 6 |
| 50 |
| 3 |
在Rt△OAC中,AC=
| OC2-OA2 |
| 40 |
| 3 |

练习册系列答案
相关题目