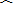题目内容
已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(1)求证:DE与⊙O相切;
(2)连结OE,若cos∠BAD=
,BE=
,求OE的长.

(1)求证:DE与⊙O相切;
(2)连结OE,若cos∠BAD=
| 3 |
| 5 |
| 14 |
| 3 |

(1)证明:如图1所示,连接OD,BD
∵AB是⊙O的直径,∴∠ADB=∠BDC=90°.
在Rt△BDC中
∵E是BC的中点,∴DE=
BC;
∴DE=BE;∴∠1=∠2.
∵OD=OB,∴∠3=∠4;
∵∠ABC=∠2+∠4=90°
∴∠ODE=∠1+∠3=90°,
即OD⊥DE,
∴DE是⊙O的切线;
(2)∵E是BC的中点,O是AB中点,
∴OE∥AC,
∴∠BAD=∠BOE,
∴cos∠BAD=∠BOE=
,
设OB=3x,则OE=5x,
∴BE=4x,
∵BE=
,
∴x=
,
∴OE=5x=
.

∵AB是⊙O的直径,∴∠ADB=∠BDC=90°.
在Rt△BDC中
∵E是BC的中点,∴DE=
| 1 |
| 2 |
∴DE=BE;∴∠1=∠2.
∵OD=OB,∴∠3=∠4;
∵∠ABC=∠2+∠4=90°
∴∠ODE=∠1+∠3=90°,
即OD⊥DE,
∴DE是⊙O的切线;
(2)∵E是BC的中点,O是AB中点,
∴OE∥AC,
∴∠BAD=∠BOE,
∴cos∠BAD=∠BOE=
| 3 |
| 5 |
设OB=3x,则OE=5x,
∴BE=4x,
∵BE=
| 14 |
| 3 |
∴x=
| 7 |
| 6 |
∴OE=5x=
| 35 |
| 6 |


练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

 45°.
45°.