Question

【题目】如图，在等边△ABC中，AB＝15，BD＝6，BE＝3，点P从点E出发沿EA方向运动，连结PD，以PD为边，在PD右侧按如图方式作等边△DPF，当点P从点E运动到点A时，点F运动的路径长是（　　）

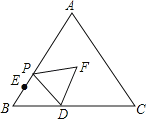
A.8B.10C.D.12

Answer 1

【答案】D

【解析】

首先利用等边三角形的性质和含30°直角三角形的运用，判定△DPE≌△FDH，△DF2Q≌△ADE，然后利用全等三角形的性质，得出点F运动的路径长.

∵△ABC为等边三角形，

∴∠B=60°，

过D点作DE′⊥AB，过点F作FH⊥BC于H，如图所示：

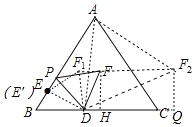
则BE′=BD=3，

∴点E′与点E重合，

∴∠BDE=30°，DE=BE=3，

∵△DPF为等边三角形，

∴∠PDF=60°，DP=DF，

∴∠EDP+∠HDF=90°

∵∠HDF+∠DFH=90°，

∴∠EDP=∠DFH，

在△DPE和△FDH中，，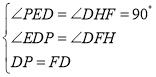

∴△DPE≌△FDH（AAS），

∴FH=DE=3，

∴点P从点E运动到点A时，点F运动的路径为一条线段，此线段到BC的距离为3，

当点P在E点时，作等边三角形DEF1，∠BDF1=30°+60°=90°，则DF1⊥BC，

当点P在A点时，作等边三角形DAF2，作F2Q⊥BC于Q，则四边形DF1F2Q是矩形，

∵∠BDE=30°，∠ADF2=60°，

∴∠ADE+∠F2DQ=180°﹣30°﹣60°=90°，

∵∠ADE+∠DAE=90°，

∴∠F2DQ=∠DAE，

在△DF2Q和△ADE中，，

∴△DF2Q≌△ADE（AAS），

∴DQ=AE=AB﹣BE=15﹣3=12，

∴F1F2=DQ=12，

∴当点P从点E运动到点A时，点F运动的路径长为12，

故选：D．