题目内容
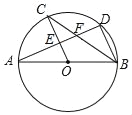
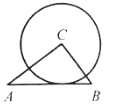
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.

【答案】(1)见解析;(2)4![]() +3.
+3.
【解析】
(1)根据两角相等的三角形相似可得出结论;
(2)先根据勾股定理求出BC的长,再由相似三角形的性质得出PE和BE的长,由勾股定理得出CE的长,进而可得出结论.
(1)证明:∵AB是⊙O的直径,BE⊥CP, ∴∠ACB=∠BEP.
∵∠CAB=∠BPC,
∴△CAB∽△EPB;
(2)∵AB=10,AC=6,
∴BC=![]() =8.
=8.
∵△CAB∽△EPB,BP=5,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴PE=3,BE=4,
∴CE=![]() =4
=4![]() ,
,
∴CP=4![]() +3.
+3.
故答案为:(1)见解析;(2)4![]() +3.
+3.

练习册系列答案
相关题目