题目内容
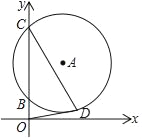
【题目】如图,以点A(1,![]() )为圆心的⊙A交y轴正半轴于B,C两点,且OC=
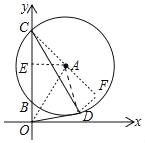
)为圆心的⊙A交y轴正半轴于B,C两点,且OC=![]() +1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )
+1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )
A. ![]() ﹣1 B. 2
﹣1 B. 2![]() C. 2
C. 2![]() D.
D. ![]() +1
+1
【答案】D
【解析】
连接OA,连接AC,过点A作AE⊥OC于E,过点D作DF⊥CF交CA的延长线于F.首先证明△AOD为等腰直角三角形,在Rt△ADF,Rt△CDF中,解直角三角形即可解决问题.
解:连接OA,连接AC,过点A作AE⊥OC于E,过点D作DF⊥CF交CA的延长线于F.
∵![]()
∴![]()
∴![]()
∴![]()
∴sin∠AOE=![]()
∴∠AOE=30°,
∴∠EAO=60°
∵AD=OD,∠ADO=90°,
∴△AOD为等腰直角三角形,
∴∠EAC=∠OAD=45°,
∴∠DAF=180°﹣45°﹣60°﹣45°=30°,
∴![]()
在Rt△CDF中,![]()
故选:D.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目