题目内容
【题目】一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.
(参考数据:![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
【答案】A距离灯塔P的距离为54.6海里.
【解析】
易知△PBC为等腰直角三角形,可得BC=PC,设BC=PC=x,则AC=20+x,在Rt△APC中,根据![]() 可得
可得![]() 推出
推出![]() 海里.在Rt△APC中,由∠A=30°,可得PA=2PC,由此即可解决问题.
海里.在Rt△APC中,由∠A=30°,可得PA=2PC,由此即可解决问题.
解:如图:
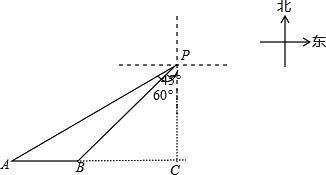
∵AC⊥PC,∠APC=60°,∠BPC=45°,AB=20,
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC,
设BC=PC=x,则AC=20+x,
在Rt△APC中,
∵![]()
![]()
∴![]() (海里).
(海里).
在Rt△APC中,
∵∠A=30°,
∴![]() (海里)
(海里)
答:A距离灯塔P的距离为54.6海里.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目