题目内容
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°. 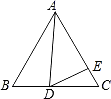
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
【答案】
(1)解:∵△ABC为正三角形,
∴∠B=∠C=60°,
∴∠ADB+∠BAD=120°,
∵∠ADB+∠CDE=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE
(2)解:∵△ABD∽△DCE
∴ ![]() ,
,
设正三角形边长为x,
则 ![]() ,
,
解得x=9,
即△ABC的边长为9
【解析】(1)根据等边三角形性质求出∠B=∠C=60°,根据等式性质求出∠BAD=∠CDE,即可证明△ABD∽△DCE;(2)由(1)知道△ABD∽△DCE,对应边成比例得出 ![]() ,列方程解答即可.
,列方程解答即可.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目