题目内容
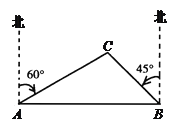
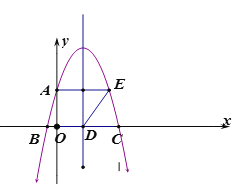
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
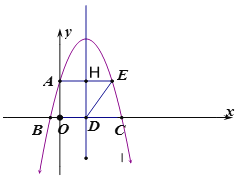
首先根据OA=![]() ,∠ABD=60°可求出OB=1,然后利用平行四边形的性质和抛物线的对称性可求出AH=1,然后可得B,C坐标,设出抛物线两点式,代入A点坐标求出a的值即可.
,∠ABD=60°可求出OB=1,然后利用平行四边形的性质和抛物线的对称性可求出AH=1,然后可得B,C坐标,设出抛物线两点式,代入A点坐标求出a的值即可.
解:设AE交抛物线对称轴于点H,易得四边形AODH为矩形,
由题意得:OA=![]() ,∠ABD=60°,AE=BD,
,∠ABD=60°,AE=BD,
∴OB=![]() ,
,
∴HE=OB=1,
由抛物线的对称性可得AH=1,
∴OD=1,
∴B(-1,0),C(3,0)
设抛物线解析式为:y=a(x+1)(x-3)(a≠0),
代入A(0,![]() )解得:
)解得:![]() ,
,
∴这条抛物线的解析式为:![]() ,
,
故选:D.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目