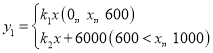��Ŀ����
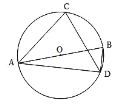
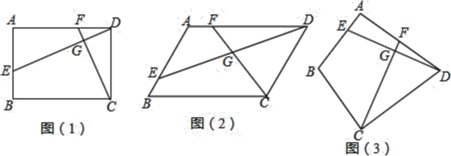
����Ŀ��ͼ����һö�ʵؾ��ȵ�����������״�����ӣ�ÿ�����Ϸֱ��������2��3��4��5��ͼ����һ�������������̣���ͨ�������ӵķ�ʽ��������Ϸ�������ǣ�����ö�����������������������������ϣ������棩�������Ǽ����ʹ�ͼ�е�A�㿪ʼ����˳ʱ�뷽�����������������㣬�ڶ��δӵ�һ�ε��յ㴦��ʼ������һ�εķ�����������
��1�������һ�����ӣ���������������C���ĸ������� ����
��2��������������ӣ��û���״ͼ���б��ķ�����������������������C���ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
��1������������Ϊ2ʱ�����Ե����C���ݴ˽�һ����⼴�ɣ�
��2�����������ӵ����ֺ�һ������2С��10����ֻ��Ҫ��һ�ܺ��C���ɣ���ʱ��Ҫ8�����ݴ˽�һ���б��ó����п����ԣ�Ȼ���ٴμ��Լ��㼴��.
��1�������һ�����ӣ���������������C����Ҫ������������������C�ĸ����൱������2���ֵĸ��ʣ�������2���ֵĸ�����![]() ��
��
�ʴ�Ϊ![]() ��
��
��2���б���ͼ��
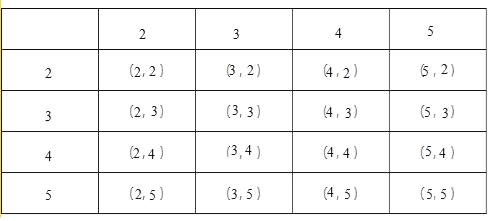
����16�ֿ��ܣ���Ϊ8���Ե����C����3�����Σ���������������������C���ĸ���Ϊ![]() ��
��

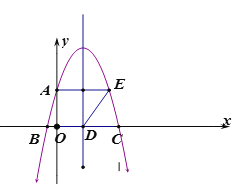
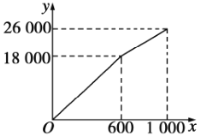
����Ŀ����֪һ�����κ���ͼ���ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ�����ʾ��
�Ķ�Ӧֵ�����ʾ��
| �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
| �� | 0 | ��3 | ��4 | ��3 | 0 | �� |
(1)��������κ����ı���ʽ��
(2)�ڸ�����ƽ��ֱ������ϵ�л���������κ�����ͼ��
(3)��![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��