题目内容
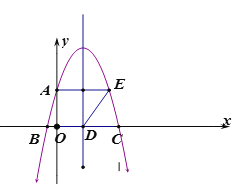
【题目】如图,在△ABC中,∠C=90°,点O、D分别为AB、BC的中点,做⊙O与AC相切于点E,在AC边上取一点F,使DF=DO.
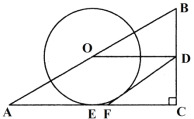
⑴求证:DF是⊙O切线;⑵若sinB=![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
【答案】(1)证明略;(2)⊙O的半径![]() .
.
【解析】
(1)作OG⊥DF于G.连接OE.先证明△OGD≌△DCF得出OG=CD,再证明四边形CDOE是平行四边形,得出OG=OE即可解决问题;
(2)由FA,FD是⊙O的切线,推出FG=FE,设FG=FE=x,由△OGD≌△DCF(AAS),推出DG=CF=2,推出OD=DF=2+x,由AC=2OD,CE=OD,推出AE=EC=OD=2+x,由sinB=![]() 推出∠A=30°,推出
推出∠A=30°,推出![]() ,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
(1)证明:作OG⊥DF于G.连接OE.
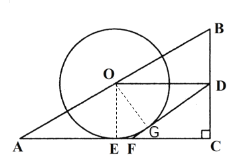
∵BD=DC,BO=OA,
∴OD∥AC,
∴∠ODG=∠DFC,
∵∠OGD=∠DCF=90°,OD=DF,
∴△OGD≌△DCF(AAS),
∴OG=CD,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠AEO=∠C=90°,
∴OE∥BC,
∵OD∥CE,
∴四边形CDOE是平行四边形,
∴CD=OE,
∴OG=OE,
∴DF是⊙O的切线.
(2)解:∵FA,FD是⊙O的切线,
∴FG=FE,设FG=FE=x,
∵△OGD≌△DCF(AAS),
∴DG=CF=2
∴OD=DF=2+x
∵AC=2OD,CE=OD,
∴AE=EC=OD=2+x
∵sinB=![]() .
.
∴∠B=60°,
∴∠A=30°,
![]()
在Rt△DCF中,∵DF2=CD2+CF2,
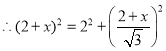
解得![]() 或
或![]()
![]()
即⊙O的半径是![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目