题目内容
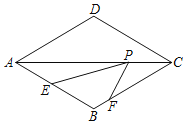
【题目】如图,在矩形ABCD中,AB=3cm,BC=4cm,P、Q两点同时从点C出发,点P沿从![]() 的方向运动,速度为2cm/秒;点Q沿从
的方向运动,速度为2cm/秒;点Q沿从![]() 的方向运动,速度为1cm/秒.当运动时间为t秒﹙0≤t≤3.5﹚时,设△PCQ的面积为y(cm2)(当P、Q两点未开始运动时,△PCQ的面积为0).则y(cm2)和t﹙秒﹚的函数关系的图象大致是( )
的方向运动,速度为1cm/秒.当运动时间为t秒﹙0≤t≤3.5﹚时,设△PCQ的面积为y(cm2)(当P、Q两点未开始运动时,△PCQ的面积为0).则y(cm2)和t﹙秒﹚的函数关系的图象大致是( )

A.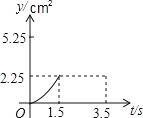 B.
B.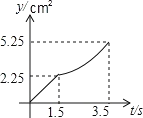 C.
C.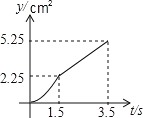 D.
D.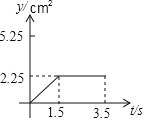
【答案】C
【解析】
本题需分点P在CD边上和点P在DA边上两种情况进行讨论,分别列出面积的表达式,根据表达式确定函数图象.
∵矩形ABCD中,AB=3cm,BC =4cm,∴CD=3cm
∴点P再CD上运动时间为:3![]() 2=1.5(秒)
2=1.5(秒)
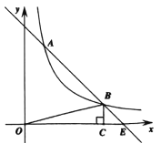
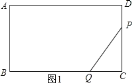
当P,Q分别在CD边和BC边上运动时,![]() ,如图1:
,如图1:
![]()
∴![]()
当P,Q分别在AD边和BC边上运动时,![]() ,如图2:
,如图2:
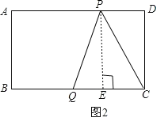
过点P作![]() 于点E,则
于点E,则![]()
∴![]()
综上可知:选项C的图象符合题意
故选:C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目