题目内容
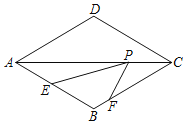
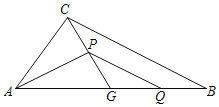
【题目】如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
(1)若α=60°,k=1,
①当BQ=![]() BG时,求∠PAG的度数.
BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
【答案】(1)①30°;②PA=PQ,见解析;(2)存在,k=![]() ,理由见解析
,理由见解析
【解析】
(1)①在GC上取点M,使得GM=GA,连接AM,再说明△AGM是等边三角形,进而得到AG=BG=2BQ,从而判定GP=MP,即AP平分∠MAG即可解答;②先说明△PGN是等边三角形,进而得到GQ=AN,从而证明△ANB≌△QGP即可解答;
(2)先说明PH=PG,∠PHA=∠PGQ=135°,得出HG=BQ,再判断出AH=GQ,进而得出△AHP≌△QGP即可.
解:(1)①如图1,在GC上取点M,使得GM=GA,连接AM,
∵∠AGM=α=60°,
∴△AGM为等边三角形,
∴AG=GM,∠MAG=60°,
∵G为AB的中点,Q为GB的中点,
∴AG=BG=2BQ,
∵k=1,
∴BQ=GP,
∴GM=AG=BG=MG=2GP,
∴GP=MP,
∴AP平分∠MAG,
∴∠PAG=∠PAM=30°;
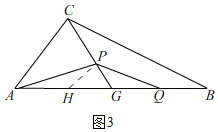
②如图2,在AG上取点N,连接PN,使得PN=PG,
∵∠PGN=60°,
∴△PGN是等边三角形,
∵BG=GA,
∴BQ=PG=PN=NG=GQ,
∴GQ=AN,
∵∠ANP=∠QGP,
∴△ANB≌△QGP(SAS),
∴PA=PQ;
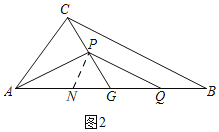
(2)存在,k=![]() ,使得②中的结论成立;
,使得②中的结论成立;
证明:如图3,过点P作PG的垂线交AG于点H.
∵∠AGC=45°,
∴∠PHG=45°,
∴PH=PG,∠PHA=∠PGQ=135°,
∵![]() ,
,![]() ,
,
∴HG=BQ,
∵AG=BG,
∴AH=GQ.
∴△AHP≌△QGP(SAS)
∴PA=PQ.


 巧学巧练系列答案
巧学巧练系列答案