题目内容
3、抛物线y=（x+3）2-2的顶点在（ ）
分析：首先根据二次函数的顶点式y=a（x-h）2+k（a≠0，且a，h，k是常数），写出顶点坐标是（h，k），然后判断顶点在第几象限．
解答：解：∵函数y=（x+3）2-2的顶点为（-3，-2），
∴顶点（-3，-2）在第三象限内．
故选C．
∴顶点（-3，-2）在第三象限内．
故选C．
点评：本题主要考查二次函数的性质的知识点，抛物线顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，正确找出抛物线的顶点坐标是解答本题的关键．
练习册系列答案
相关题目
A和C，和x轴的另一个交点为B．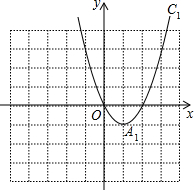
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．