题目内容
【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
A. ∠E=∠FB. ∠E+∠F=180°
C. 3∠E+∠F=360°D. 2∠E-∠F=90°
【答案】C
【解析】
直接利用平行线的性质得出∠ABE+∠CDE=∠BED,进而利用四边形内角和定理得出2∠BED+∠BED+∠F=360°,即可得出答案.
解:过点E作EN∥DC,
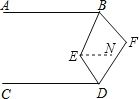
∵AB∥CD,
∴AB∥EN∥DC,
∴∠ABE=∠BEN,∠CDE=∠NED,
∴∠ABE+∠CDE=∠BED,
∵∠EBF=2∠ABE,∠EDF=2∠CDE,
∴设∠ABE=x,则∠EBF=2x,设∠CDE=y,则∠EDF=2y,
∵2x+2y+∠BED+∠F=360°,
∴2∠BED+∠BED+∠F=360°,
∴3∠BED+∠F=360°.
故选:C.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目