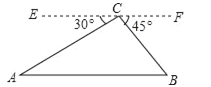
题目内容
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探宄问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数n,我们进行如下操作:
(1)将n拆分为两个正整数m1,m2的和,并计算乘积m1×m2;
(2)对于正整数m1,m2,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即折分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,
请探究不同的拆分方式是否影响正整数n的“神秘值”,并说明理由.
(尝试探究):

(1)正整数1和2的“神秘值”分别是
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
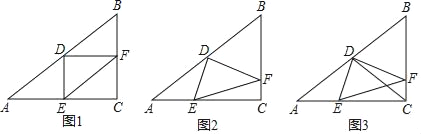
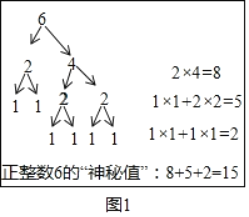
如图所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在如图中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在如图中绐出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数n的“神秘值”与其折分方法无关.请帮助小凯,利用尝试成果,猜想正整数n的“神秘值”的表达式为 ,(用含字母n的代数式表示,直接写出结果)
【答案】(1)1,1;(2)n的神秘数是![]() (n>1)
(n>1)
【解析】
(1)根据神秘数的定义,将正整数分解,求和即可;
(2)将6和7分解,直到不能分解位置,再将所有的乘积求和即可;
结论猜想:找出多个数的神秘数,再找出规律即可.
(1)根据“神秘数”的定义,1不能在分,
∴1的神秘数是1,
∵2可以分为1和1,
∴2的神秘数是1,
故答案为:1,1;
(2)如图所示:
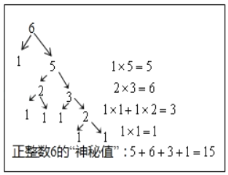
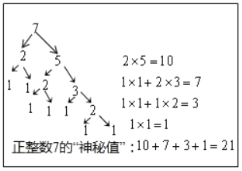
结论猜想:
∵3的神秘数是3,4的神秘数是6,5的神秘数是10,6的神秘数是15,7的神秘数是21,…,
∴n的神秘数是![]() (n>1).
(n>1).

【题目】某自行车厂计划一周生产1400辆自行车,平均每天生产200辆,由于各种原因,实际每天的生产量与计划量相比有出入。
下表是某周的生产情况(超产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产了_________辆;
(2)产量最多的一天比产量最少的一天多生产__________辆;
(3)该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?